Logicollege

We noemden dit al in Module 5, maar gaan er hier wat dieper op in. Onderstaande grafiek (Error! Reference source not found.) zal je inmiddels bekend voorkomen. Het is de grafische weergave die behoort bij de formule van Camp. In de grafiek zie je door het dal van de kromme bij welke seriegrootte de totale kosten het laagst zijn.

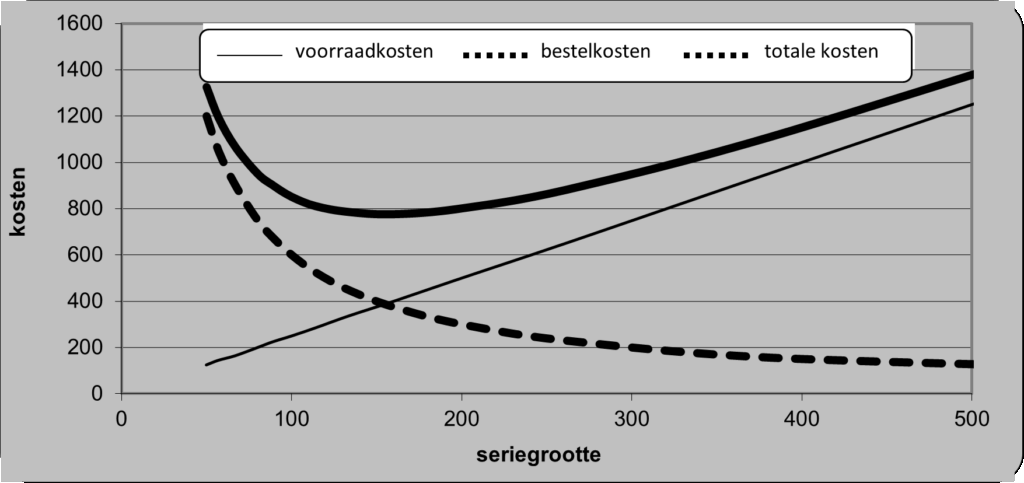
figuur 1: afweging van voorraadkosten

Als je het model wilt hanteren, moet je de kostenfactoren kennen. Om een nauwkeurig resultaat te bereiken zou je de voorraadkosten en de bestelkosten nauwkeurig moeten bepalen, maar in de praktijk valt dat niet mee. De vraag welke kosten worden beïnvloed door je beslissing, geeft vaak aanleiding tot stevige discussie over de factoren die je wel of niet moet meenemen. En vervolgens ontstaat discussie over de hoogte van die kostenfactoren.

Is daarmee de formule van de baan? We gaan eerst maar eens naar de gevoeligheid van de uitkomsten van de formule kijken en concentreren ons daarna op de gevoeligheid van de kostenfactoren.

Aan het verloop van de lijn van de totale kosten in figuur  kun je zien dat in dit geval de meerkosten niet erg groot zijn als je een beetje zou afwijken van de optimale seriegrootte. Ook uit de cijfers van tabel 1 kwam dit al naar voren.

In dit voorbeeld loopt het dal van totale kostenlijn vrij vlak. In de buurt van het laagste punt is een tamelijk breed gebied vlak. In onderstaande tabel zie je wat de meerkosten zijn, als je afwijkt van de optimale seriegrootte.

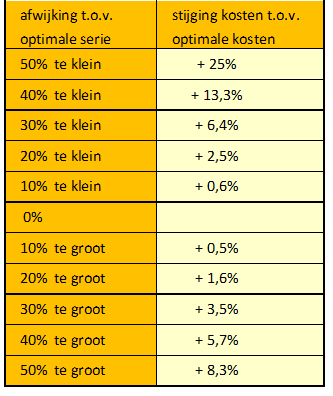
tabel 3: extra kosten bij afwijking van de optimale serie

Uit bovenstaande tabel (tabel 3) kun je afleiden dat je slechts een verhoging van 2,5% van de beïnvloedbare totale kosten veroorzaakt door te kiezen voor een serie die 20% kleiner is dan de optimale. Als je voor een serie kiest die 20% groter is dan de optimale dan nemen je totale kosten zelfs maar toe met 1,6%.

Als je de berekende optimale seriegrootte om een praktische reden, boven of naar beneden wilt afronden, dan zou je in dit voorbeeld (met de gegevens uit tabel 3) het best kiezen voor een afronding naar boven. Let op, dat is niet altijd zo, in de meeste gevallen kun je beter naar beneden afronden, want de werkelijke kosten van de extra order die daardoor ontstaat zijn meestal verwaarloosbaar, terwijl de rentekosten van extra voorraad wel direct van toepassing zijn. Het is (bijna) altijd handig voor de kosten van opslag of transport, om je bestelling af te ronden op hele verpakkingseenheden of op een hele transporteenheid. Of bij een productieorder, om die af te ronden op een geheel aantal maal de technisch vereiste omvang van een productiebatch, in verband met de standtijd van het gereedschap (matrijzen, gietmallen, walsen etc.).

Bij de beslissing over het afronden van de berekende seriegrootte, moet je er wel op bedacht zijn dat je berekening geldt voor een bepaalde situatie, die als input in het model wordt vastgelegd met de getallen voor D, F, α en K. Als je bijvoorbeeld een hoger rendement op het geïnvesteerde vermogen wil (of moet) en daarvoor de factor α verhoogt, dan gaat de C_v-lijn steiler lopen en daarmee verandert de C_tot-lijn. Hoe steiler het rechterdeel van de C_tot-lijn loopt, des te gevoeliger wordt de seriegrootte voor een afwijking naar boven. Ook kunnen fysieke factoren spelen, waardoor de seriegrootte aan een bovengrens wordt gebonden. Denk bijvoorbeeld aan het laadvermogen van een zeecontainer, vrachtauto of spoorwagon.

Als één van de kostenfactoren in werkelijkheid 100% hoger zou zijn dan het getal dat je hebt ingevuld in de formule, dan geeft dat een afwijking in je optimale serie van 44%. Als je je ‘maar’ 50% zou hebben vergist, dan is de fout in de berekende optimale serie maar 22% en bij een afwijking van 25% in de kosten nog maar 12%. Omgekeerd geldt, dat de kostenfactoren dus maar een beperkte invloed hebben op de berekende EOQ.  

Ook al heb je dus een onzekerheid in de kosten waar je mee rekent, met de formule van Camp kom je toch op een seriegrootte die in de buurt komt van het echte optimum. Omdat het dal in de totale kostenlijn erg vlak is, zal je berekening meestal tamelijk dicht bij de minimale kosten uitkomen, ondanks de afwijking in je kostenfactoren.

De conclusie is, dat zelfs als je de kostenfactoren niet helemaal juist kunt vaststellen, de formule je nog steeds een bruikbaar resultaat levert.
Dat betekent dus niet, dat je met willekeurige input ook tot een aanvaardbaar resultaat komt.