Logicollege

Het EOQ-model heeft nogal wat randvoorwaarden. Door het model een beetje uit te breiden, kan aan sommige van die randvoorwaarden worden voldaan.

Sommige randvoorwaarden kunnen in de formule worden ingebouwd in de vorm van een correctiefactor. Bijvoorbeeld als je te maken hebt met een verschil tussen productie- en verbruikssnelheid of als er een kostbare voorraad onderhandenwerk (OHW) gedurende lange tijd in bewerking is. In de volgende paragrafen beschrijven we een aantal van deze aanvullingen op het model.

6.1. De invloed van de productiesnelheid

In de praktijk zal fabricage van een productieserie tijd kosten. Een randvoorwaarde van Camp, is dat de geproduceerde goederen pas beschikbaar zijn, als de gehele serie gereed is. In de praktijk zal het vaak voorkomen dat de serie al in gedeelten beschikbaar komt, tijdens de fabricage van de rest van de serie. De serie wordt dan in delen (of zelfs stuk voor stuk) aan de beschikbare voorraad gereed product toegevoegd. De redenen waarom je verbruik tijdens productie toe laat kunnen zijn:

• reductie van de voorraad,
• reductie van de doorlooptijd,
• reductie van de hoeveelheid OHW in een productieproces dat uit meerdere schakels bestaat.

Deze redenen spelen vooral sterk, als er sprake is van:

• een volumineus of kostbaar artikel,
• een betrekkelijk langdurig fabricageproces, of
• een per tijdseenheid relatief grote vraag.

Als je verbruik tijdens productie toe laat, heeft dat tot gevolg dat een gedeelte van je productie-order al aan klanten geleverd kan zijn voordat je gehele serie gereed is. Bij een seriegrootte Q* zal de voorraad gereed product daardoor niet Q*-eenheden toenemen, maar met minder. Het verschil is afhankelijk van de verhouding tussen verkoopsnelheid (V) en productiesnelheid (P), dus afhankelijk van (V/P).

We laten een dergelijke situatie in grafiekvorm zien in onderstaande figuur.

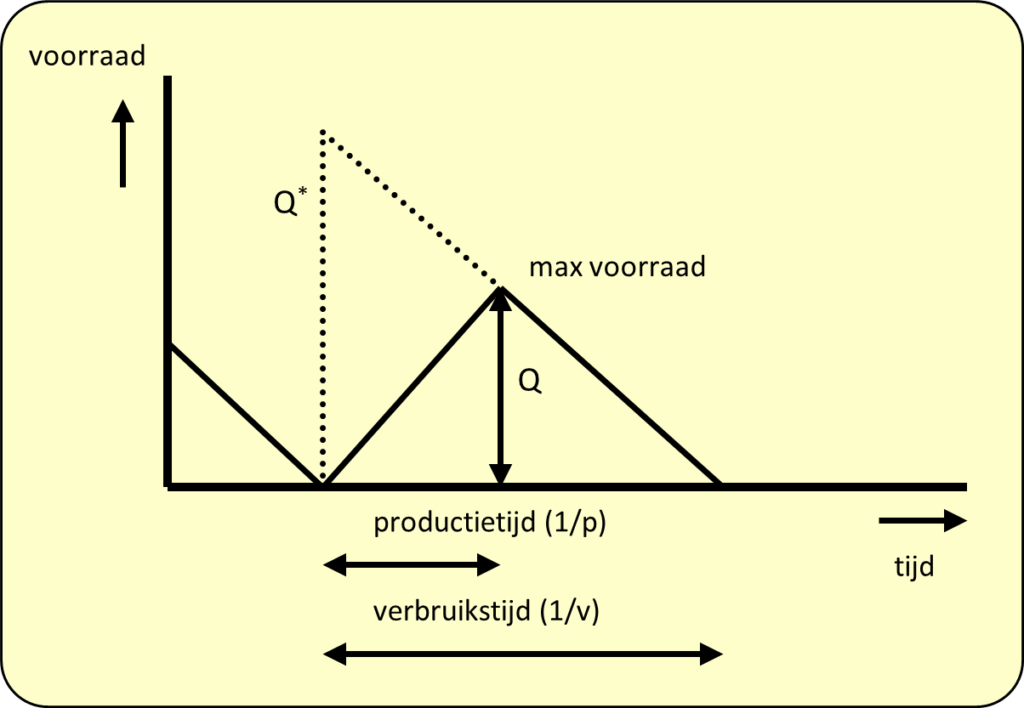
figuur 2: voorraadverloop bij een verschil in productie- en verkoopsnelheid

Doordat niet de gehele productieserie tegelijk beschikbaar komt en er tussentijds reeds uit wordt verkocht, wordt in de formule voor de voorraadkosten een correctiefactor aangebracht: (C_v) = ½Q_opt x (1-V/P) x aK. Als je deze formule combineert met de formule van de orderkosten, stel je de formule voor de totale kosten samen. Door net als bij de ‘gewone’ formule de kostenformule te differentiëren en vervolgens op nul te stellen, krijg je de formule voor het optimum.

De aldus gecorrigeerde formule voor de berekening van de seriegrootte wordt:

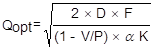
Hierin is:

Q_opt = optimale seriegrootte (Q*)

D     = jaarverbruik

F     = orderkosten per serie

V     = verbruik in stuks per periode

P     = productie in stuks per periode

a    = factor voorraadkosten per jaar

K     = kostprijs per stuk

In de nieuwe formule kun je de oorspronkelijke formule van Camp herkennen, met daarin de correctie van de voorraadkosten met de term (1 – V / P). We zullen je hier de afleiding van de formule besparen, maar de werking toelichten met een voorbeeld.

Voorbeeld

FijnSpees verkoopt onder de merknaam RedHot chilikruiden om dipsausen mee te maken. Jaarlijks worden er 25.000 potjes van het product verkocht. Om de potjes te produceren is een automatische meng-vulinstallatie gekocht, die ook geschikt is om andere mengsels te maken. Jaarlijks kan de installatie 150.000 potjes met willekeurig mengsel mengen en vullen. Het omstellen van de machine kost enige tijd, omdat de hele installatie moet worden schoongemaakt. De planner gaat uit van € 150 per omstelling. De kosten van voorraad houden zijn 15%, terwijl de fabricagekostprijs van het artikel € 3,25 per eenheid bedraagt. Tijdens productie van een nieuwe serie wordt er direct al van verkocht. Wat is nu de optimale bestelserie.

De maximale voorraad zal nooit de omvang van de optimale bestelserie bereiken. Belangrijk is de verhouding V/P. Deze verhouding is in dit geval 25.000/150.000 of te wel: 1/6. Als je dit invult in de formule krijg je:

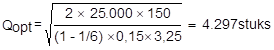
Als de productiesnelheid vele malen hoger ligt dan de verkoopsnelheid, zoals in bovenstaand voorbeeld van FijnSpees, dan zal de verhouding V/P bijna gelijk zijn aan 0. In zo’n geval komt de ‘gecorrigeerde’ optimale bestelserie dan dicht bij de ‘normale’ optimale bestelserie.

In de (theoretische) situatie waarin de productiesnelheid ongeveer even groot is als de verkoopsnelheid, zal de economische seriegrootte oneindig groot worden, omdat de term (1-V/P) in de noemer van de breuk dan (bijna) 0 wordt. Dat klopt natuurlijk, want er zal in dit geval voortdurend precies verkocht worden wat de machine kan maken zolang hij blijft draaien.

6.2. De invloed van de voorraad onderhandenwerk

Het model van Camp gaat ervan uit dat de afname van de voorraad min of meer gelijkmatig verloopt en dat aanvulling in series plaatsvindt. Alleen de gemiddelde voorraad ter grootte van ½Q wordt in het model meegenomen. De aanname is dat pas voorraadkosten ontstaan als de serie gereed is en aan het magazijn is geleverd. Maar in productiebedrijven is er ook andere voorraad…

Je haalt je grondstoffen en materialen meestal ruim op tijd in huis, onder andere om leegloop van machines te voorkomen. Ruim op tijd wil zeggen te vroeg, je hebt dan meer voorraad in huis dan nodig. Stel dat een bedrijf de gewoonte heeft om grondstoffen twee weken voor aanvang van de feitelijke productie binnen te laten komen, om er zeker van te zijn dat ze alles op tijd binnen hebben. Deze bestelpolitiek zal, onafhankelijk van de grootte van de productieserie, altijd tot twee weken extra voorraad grondstof leiden. Deze extra voorraad is een gevolg van een beslissing met een andere doelstelling (veiligheid inbouwen) en mag dus geen invloed uitoefenen op de seriegroottebepaling. Blijft dus buiten het model voor de EOQ.

Anders wordt de situatie als je een productieorder hebt opgestart en deze een betrekkelijk lange tijd in de productie verblijft. De doorlooptijd is lang, als de order bijvoorbeeld meer productiefasen na elkaar moet doorlopen, misschien onderbroken door bijvoorbeeld drogen of afkoelen, maar ook dat zijn ‘productiestappen’. Er is dan een voorraad OHW aanwezig waarvan de hoogte afhankelijk is van de seriegrootte en van de doorlooptijd in de productie.

Om leegloop te voorkomen wordt vaak alvast begonnen met de productie van de benodigde onderdelen, voordat ze in de volgende productiefase nodig zijn. Die sla je op in de vorm van halffabricaat. Er ontstaan wachttijden in het proces en die kunnen vooral oplopen, als je machines een hoge bezettingsgraad hebben. Hoewel het vanuit financiële overwegingen juist heel goed kan zijn dat je een machine zo in gaat plannen dat deze een hoge bezetting heeft, heeft dit als nadeel dat er ‘files’ in je fabriek ontstaan van halffabricaat dat wacht op capaciteit in de volgende productiefase. Door deze files ontstaan vergissingen met als gevolg nog meer voorraden halffabricaat op de werkvloer.

De wachttijden worden onevenredig veel langer als je werkt met grote series op installaties met een hoge bezettingsgraad. Als je een serie op een bepaalde machine moet worden bewerkt, dan is bij een hoge bezettingsgraad de kans groot dat er al een andere serie op die machine wordt bewerkt en moet worden gewacht tot die gereed is.  Bij grote series kan het lang duren voor die machine vrij is.

Voorbeeld

Eén van de producten van CleanPower is shampoo. De shampoo wordt afgevuld in series ter grootte van Q flessen. Daarna gaat de partij in haar geheel naar de etiketteermachine. Dit is de laatste bewerking in productie. Van de etiketteermachine gaat de partij naar het magazijn gereed product.

CleanPower investeert dus zowel in voorraad onderhandenwerk als in eindproduct.

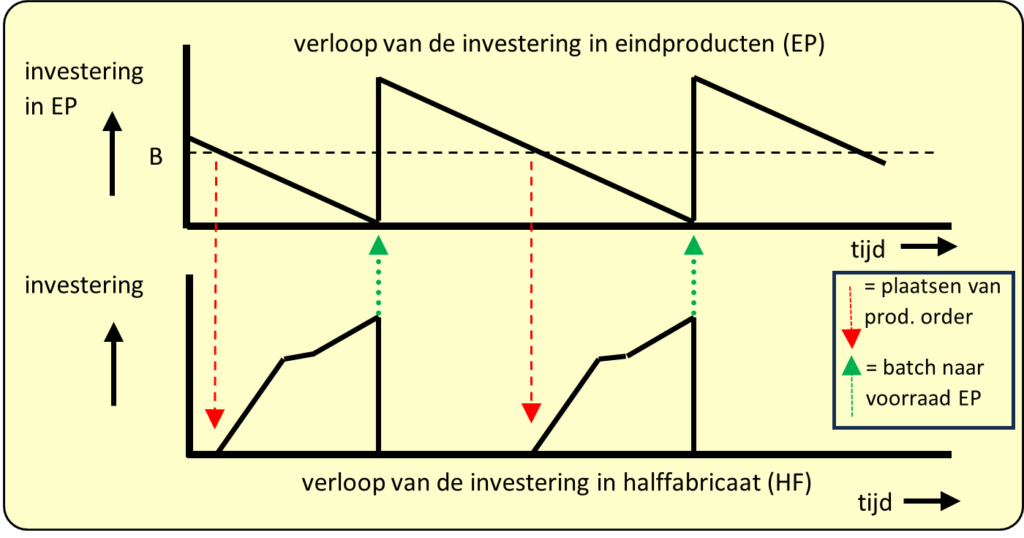
figuur 3: voorbeeld van het verloop van de investering in eindproduct en in halffabricaat

De omvang van de investering in voorraad OHW wordt mede bepaald door de seriegrootte. De kosten die met de voorraad OHW samenhangen, zou CleanPower dus ook mee moeten nemen bij de bepaling van de optimale seriegrootte. Zonder verder rekenwerk kun je al begrijpen, dat de voorraad OHW tot gevolg zal hebben dat de optimale serie waarin CleanPower produceert, kleiner moet zijn dan de uitkomst van de ‘normale’ formule van Camp.
In het verloop van de investering in halffabricaat, zie je in figuur 13 een klein stukje horizontaal verlopen. Dat is de wachttijd tussen de vulmachine en de etiketteermachine, waarin de waarde van het product niet toeneemt.

In het rekenmodel voor de seriegrootte zullen we op de een of andere manier tot uitdrukking moeten brengen dat de voorraadkosten van het OHW afhankelijk zijn van de doorlooptijd (dlt). Die is echter op zijn beurt weer afhankelijk is van de seriegrootte.

De oplossing is rekenen door met de gemiddelde productietijd per eenheid.  We geven die de letter f. De gemiddelde doorlooptijd vind je door de fabricagedoorlooptijd van een serie te delen door het aantal eenheden in die serie.
In formulevorm is de doorlooptijd voor fabricage van een serie Q dan:

                                                   dlt  =  f x Q

waarin:

Q = seriegrootte

f   = gemiddelde productietijd per eenheid product.  

Als je kiest voor een grote serie (Q), wordt de doorlooptijd van de serie langer dan bij een kleine waarde van Q.

Voor de productietijd neem je het totaal van de omsteltijd plus de bewerkingstijd plus de (gemiddelde) wachttijd.  

De waarde van een artikel neemt gedurende de productie toe van grondstofwaarde tot de kostprijs van het eindproduct. Hoe hoog de gemiddelde waarde is tijdens het fabricageproces, hangt dus af van de begin- en eindwaarde, maar hangt ook af van het verloop van de waardetoename in het proces. Als de waarde gelijkmatig toeneemt, is de gemiddelde waarde van een eenheid product, gelijk aan de helft van de waarde van de grondstoffen plus de helft van de waarde van het eindproduct: ½ x (waarde GS + waarde EP).

Als de waardeopbouw tijdens het fabricageproces niet gelijkmatig verloopt, heeft dat invloed op het gemiddelde: als direct aan het begin van het proces al een groot deel van de waarde wordt opgebouwd neemt de gemiddelde waarde toe. Het gemiddelde wordt lager als de grootste waarde opbouw pas aan het eind van het traject plaats vindt.

In het model willen we rekening houden met eventuele ongelijkmatigheid in de waardeopbouw.  Dat doen we door het invoeren van een percentage (h) dat we toepassen op de kostprijs van het eindproduct. De waarde van h kiezen we als percentage tussen 0 en 100. Die vermenigvuldigen als factor met de kostprijs van het EP. Let op, als factor ligt h tussen 0 en 1. De gemiddelde waarde van een eenheid OHW wordt dan h x K.

De voorraadkosten per eenheid gereed product hadden we in het model van Camp uitgedrukt als a x K. Op dezelfde manier uitgedrukt, worden de voorraadkosten voor het OHW dus:

C_v =  a x h x K.

Bij gelijkmatige opbouw van de waarde in het proces, is h gelijk aan 0,5. Wordt alle waarde direct aan het begin opgebouwd, dan is h 1 en als het product pas helemaal aan het eind van het proces in waarde zou stijgen, dan is h gelijk aan 0. Maar we zijn er nog niet …

Het gedeelte van een jaar dat het product als OHW in bewerking is, kun je berekenen door het aantal eenheden dat per jaar moet worden geproduceerd (D), te vermenigvuldigen met de productietijd per eenheid (f). De hoeveelheid die gedurende die tijd aanwezig is als OHW, is gelijk aan één serie (Q). De gemiddelde voorraad OHW is dan:

gem. voorraad OHW = D x f x Q.

Daarbij moet je wel opletten dat D en f in dezelfde tijdseenheid worden uitgedrukt. D staat (meestal) uitgedrukt als de vraag per jaar. Als je voor f ook een jaar als tijdseenheid neemt, zal f een heel klein getalletje worden.

Om de voorraadkosten van het OHW te bepalen, vermenigvuldig je de gemiddelde voorraad (D x f x Q) met de voorraadkosten per eenheid product: a x h x  K .

De voorraadkosten van het OHW op jaarbasis zijn gelijk aan de gemiddelde voorraadhoogte maal de voorraadkosten per eenheid, of in formulevorm:

f     =       (gemiddelde) fabricagedoorlooptijd van één eenheid product

h    =       h is afhankelijk van de waarde opbouw in het proces en ligt tussen 0 en 1. Het is de fractie van de kostprijs waarmee je de gemiddelde waarde van het product bepaalt gedurende het productieproces.

De voorraadkosten van de gemiddelde voorraad eindproducten zijn: ½ Q x aK.

Het bestellen kost per jaar: D/Q x F.

De totale kosten in het aangevulde EOQ-model bestaan uit de voorraadkosten van het onderhandenwerk vermeerderd met de kosten van de voorraad gereed product plus de bestelkosten. In formulevorm komen we uit op:

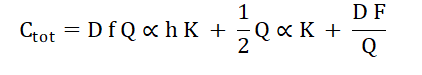
Door bovenstaande formule te differentiëren naar Q en vervolgens de afgeleide functie op nul te stellen, onstaat een gecorrigeerde formule van Camp. De afleiding verloopt net zoals die voor de basisformule (zie hoofdstuk 1), dus die slaan we hier over.

We hebben nu een model voor de gevallen waarin rekening moet worden gehouden met een voorraad OHW: De formule voor de optimale seriegrootte Q_OHW.

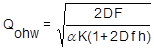
In de formule zil je de oorspronkelijk formule van Camp nog herkennen, je ziet de correctie op de voorraadkosten ter grootte van de factor (1 + D f h).

Uit de formule kun je afleiden dat de optimale serie Q_ohw kleiner wordt als:

• de waarde van de voorraad onderhandenwerk al vroeg in het proces sterk toeneemt (grote factor h);
• de doorlooptijd van de productie langer wordt (grote factor f).