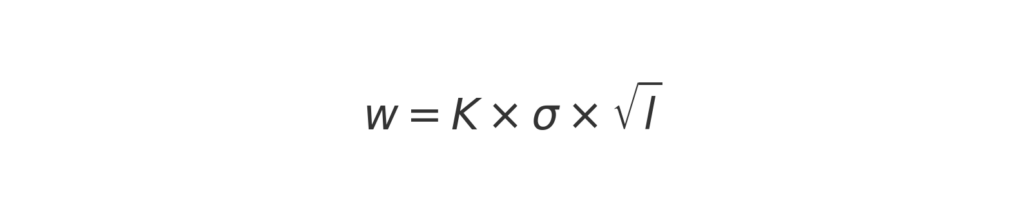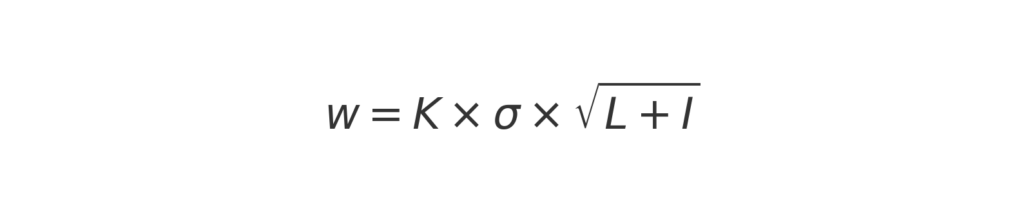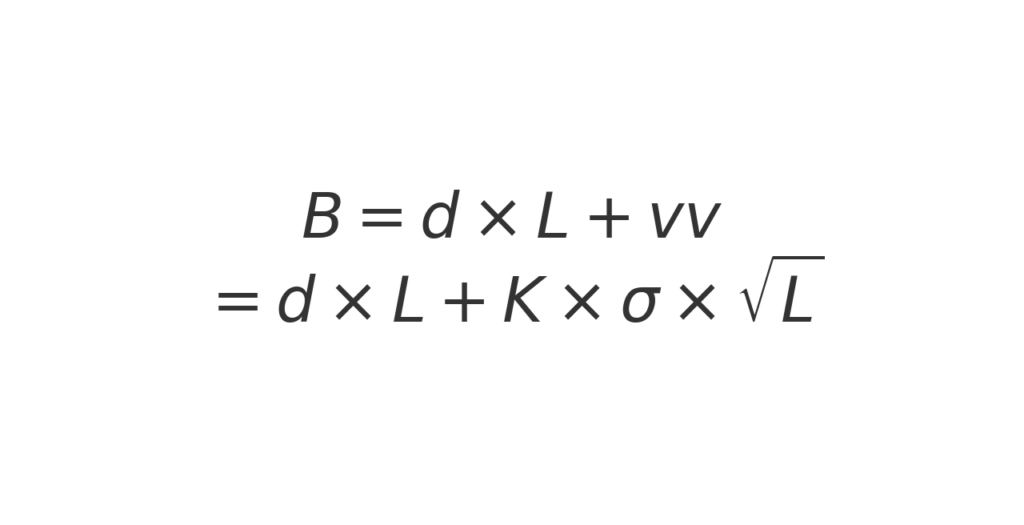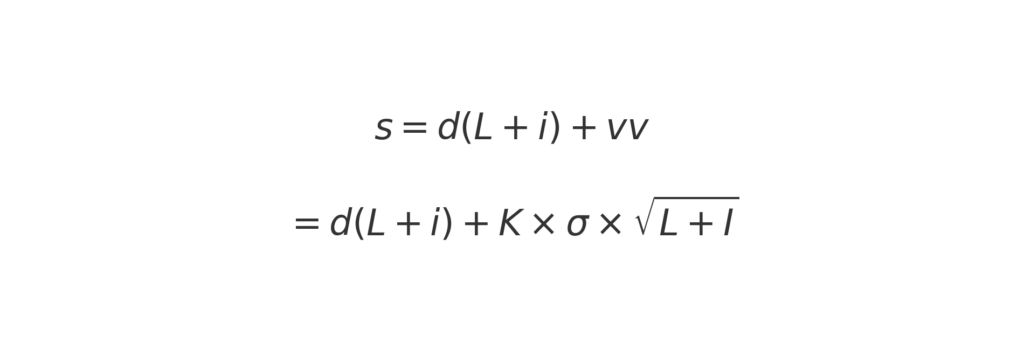In de verdieping van deze module kun je de uitleg vinden over de achterliggende statistiek, hier beperken we ons tot de formules.

Voor het berekenen van de veiligheidsvoorraad is het nodig om een maatstaf te hanteren voor de variatie in de vraag. Een daarvoor geschikte maatstaf is de standaardspreiding (standaard deviatie), meestal weergegeven met de griekse (kleine) letter sigma: σ.

De formule waarmee je de veiligheidsvoorraad kunt berekenen is:

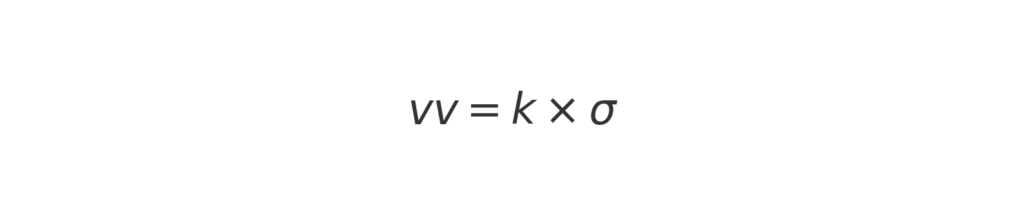
waarin:

vv:      veiligheidsvoorraad

k :       veiligheidsfactor, afhankelijk van het gewenste serviceniveau

s :       standaarddeviatie van de vraag gedurende de leadtime

Omdat je meestal zult werken met een s die is gebaseerd op vaste historische periodes (bijvoorbeeld week- of maandgegevens, die niet geheel zullen overeenkomen met de lengte van de leadtime), passen we de formule voor de VV aan aan de periode waarop de onzekerheid betrekking heeft. Dat doen we door de uit de historische gegevens gemeten σ te vermenigvuldigen met de wortel uit de leadtime:

Deze methode is geschikt oor een B-systeem, want de onzekerheidsperiode gaat hier in op het moment dat de voorraad onder B komt en eindigt op het moment van beschikbaarheid van de levering.

Bij een s-systeem is de periode van onzekerheid langer, want het zou goed kunnen dat de voorraad nog maar net boven het s-niveau is op bepaald bestelmoment (en je dus niet gaat bestellen). Omdat het even duurt voor er weer een bestelmoment is, is de periode van onzekerheid groter. In een s-systeem telt ook het bestelinterval mee. In formulevorm wordt de berekening van de VV in een s-systeem als volgt:

Hierin is:

k = veiligheidsfactor

s = de standaarddeviatie per standaard periode

L = leadtime

i  = bestelinterval

De complete formules voor de bestelniveaus ‘B’ en ‘s’ worden als volgt:

waarin:

L = de gemiddelde levertijd

d = de te verwachten gemiddelde afname per tijdseenheid

s = standaarddeviatie

k = veiligheidsfactor

i = bestelinterval