Logicollege

In dit hoofdstuk leren we je werken met een rekenmodel, een veiligheidsvoorraad (VV) kunt berekenen die groot genoeg is om je gewenste servicegraad te realiseren. Je hebt in de vorige paragraaf kunnen zien, dat de kansverdeling van de vraag vaak (ongeveer, redelijk) overeenkomt met de normale verdeling. Die gebruiken we in het rekenmodel.

Als je voor je bestelniveau alleen maar uitgaat van de gemiddelde vraag en je niet indekt tegen mogelijke afwijkingen ten opzichte van dat gemiddelde, dan loop je 50% kans dat klanten meer dan het gemiddelde willen kopen tijdens de leadtime. Je loopt een kans op nee-verkoop van 50%. Als je veiligheidsvoorraad gaat inbouwen in je bestelniveau, verminder je het risico op nee-verkopen.

Inbouwen van veiligheidsvoorraad komt overeen met kiezen van een punt rechts van het gemiddelde op de X-as in de grafiek van de normale verdeling. De afstand tot het gemiddelde is een maatstaf voor je risico. Je kunt aan de grafiek zien hoeveel kans er is dat er meer dan die waarde gevraagd zal worden. In statistische termen: hoe groter de excentriciteit, (het aantal malen de standaarddeviatie als afstand van het gemiddelde), hoe kleiner de overschrijdingskans. Hoe kleiner je risico, des te kleiner is het resterende oppervlak rechts in de grafiek. Dus hoe meer naar rechts, hoe groter k, hoe kleiner je kans op nee-verkoop.

Als je een doelstelling zou hebben voor je maximale risico van nee-verkoop, dan kun je die doelstelling omdraaien tot een norm voor de gewenste servicegraad. Vervolgens kun je de grootte van de aan te houden veiligheidsvoorraad berekenen. Dat doe je met een tabel met rechteroverschrijdingskansen van de normale verdeling.

Als je 0,13% nee-verkoop zou accepteren of, omgekeerd, als je een servicegraad van 99,87% nastreeft, dan heb je een veiligheidsvoorraad nodig van 3s. Immers in paragraaf 15.4.2 kon je zien dat de overschrijdingskansen bij een k van nul, één, twee- en driemaal de standaarddeviatie (s) voor de normale verdeling respectievelijk 50%, 15,87% 2,28% en 0,13% waren.

Toegepast op voorraadbeheer betekent dit:

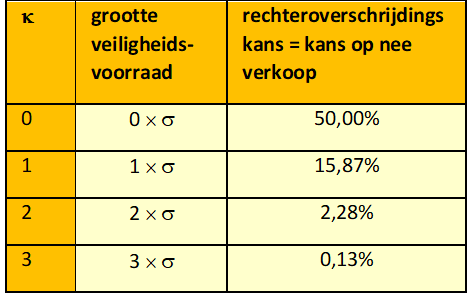
tabel 4: veiligheidsvoorraad en kans op nee-verkoop

Als je een veiligheidsvoorraad aanlegt ter grootte van 1 x σ, vermindert je risico op nee-verkoop met (50% – 15,87%) = 34,23%. Vergroot je de veiligheidsvoorraad vervolgens tot 2 x σ dan krijg je een verdere verbetering van je servicegraad met (15,87% – 2,28%) = 13,59%. Als je de veiligheidsvoorraad opvoert tot 3 x σ, dan wordt je risico op nee-verkoop nog een stukje kleiner, gaat dan van 2,28% naar 0,13% en wordt dus 2,15% kleiner. Met een stap naar 4 x σ, neemt je servicegraad nog maar een heel klein beetje toe. In het voorraadbeheer zul je meestal kiezen voor een veiligheidsfactor (κ) ergens tussen 2 en 3, afhankelijk van het commerciële belang van de servicegraad, van de kosten van nee-verkoop.

resumerend:

De kans dat je gedurende de leadtime meer verkoopt dan de hoeveelheid μ + κ x σ en dus nee moet verkopen, wordt bepaald door het oppervlak van de kromme, dat rechts van
 μ + κ x σ ligt.

Hierin is μ de gemiddelde vraag die je tijdens de leadtime kunt verwachten.

Als je de kans op nee-verkoop wilt beperken, moet je bovenop de benodigde voorraad voor de verwachte vraag gedurende de leadtime, een veiligheidsvoorraad aanleggen ter grootte van k maal de standaarddeviatie (s). Waarbij de factor ‘k’ afhankelijk is van de servicegraad die je aan klanten wilt bieden. In formulevorm:

vv = κ x σ

waarin:

vv:       veiligheidsvoorraad

k :        veiligheidsfactor

σ :        standaarddeviatie van de vraag gedurende de leadtime

 

Voorbeeld

Voor olijfzeep, verpakt in vaatjes van 5L is de te verwachten tijdens de leadtime vraag 50 stuks. Ddat wil in dit geval zeggen gedurende de tijd die nodig is voor de productie van een charge (serie, batch). Uit historische gegevens blijkt een standaarddeviatie van 4 stuks over deze periode. Hoeveel veiligheidsvoorraad moet er liggen om niet meer dan 6,7% risico te lopen om buiten voorraad te raken? In de tabel in bijlage 1 kun je aflezen, dat een overschrijdingskans van 6,7% overeenkomt met een k-waarde (veiligheidsfactor) van 1,5. Dit betekent dat een veiligheidsvoorraad van 1,5 x 4 stuks = 6 stuks voldoende is voor de gevraagde 6,7% kans op nee-verkoop.

De overschrijdingskans bij de 1,5 x σ uit het voorbeeld, de kans op een vraag groter dan een bepaald aantal, hebben we weergegeven in Figuur9. Het is het oppervlak van de kansverdeling rechts vanaf X=56 (tot het oneindige).

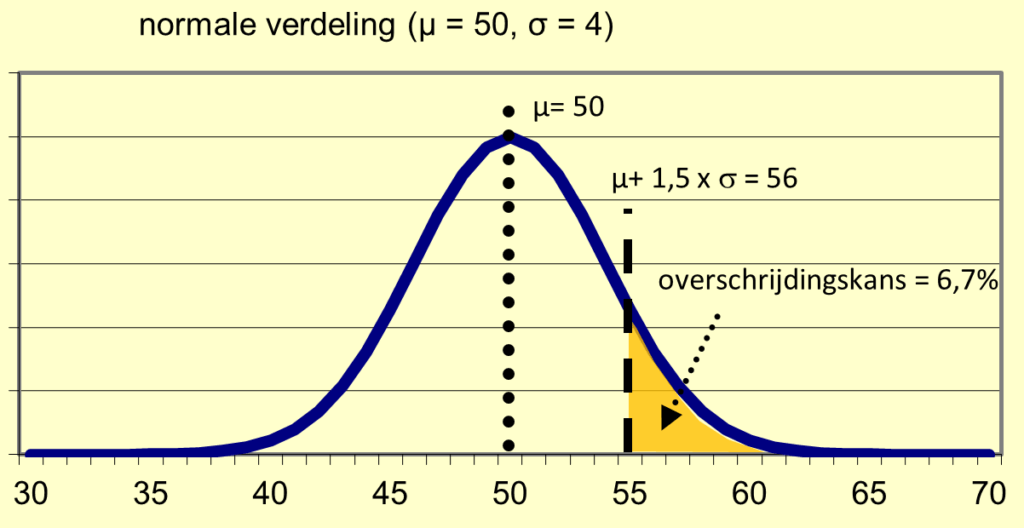
Figuur 9: overschrijdingskans bij de normale verdeling

Voor het berekenen van de vv hadden het tot nu toe over de vraag gedurende de leadtime. Daar gaat het om bij het bepalen van je veiligheidsvoorraad. Als we te maken krijgen met een langere leadtime (bijvoorbeeld een andere leverancier met lagere prijs, maar met een langere leadtime), moeten we de vraag gedurende een grotere periode gaan beschouwen. Om dezelfde servicegraad te kunnen realiseren moet je de vv herberekenen door zowel de gemiddelde vraag als ook de standaarddeviatie aan te passen. Als de leadtime toeneemt, zal de vv groter moeten worden.

De vraag gedurende de leadtime

De (gemiddelde) vraag gedurende de leadtime is recht-evenredig met de lengte van de leadtime: bij een tweemaal zo lange periode hoort een tweemaal zo grote gemiddelde vraag. Als een maand 4 weken zou hebben, dan is de gemiddelde vraag per maand 4 x de gemiddelde vraag per week.

De standaarddeviatie gedurende de leadtime

Met de langere leadtime neemt de periode van onzekerheid toe. Algemeen geldt, dat hoe groter de periode van onzekerheid is, des te groter de standaard spreiding van de vraag (gedurende die periode) zal zijn. De toename van de spreiding is niet recht-evenredig met de toename van de lengte van de periode. De toename van de spreiding komt overeen met de wortel uit de factor waarmee de periode is vergroot (of verkleind). Dus bij bijvoorbeeld een 2x zo lange leadtime, neemt de spreiding toe met √2.

De herberekening van μ en σ samengevat in een voorbeeld:

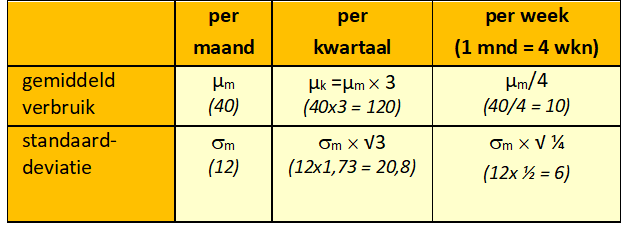
tabel 5: herberekenen van gemiddelde en spreiding voor een grotere of kleinere leadtime

In de administratie van je bedrijf, zul je verkoopgegevens (hopelijk ook vraagcijfers) vinden, voor vastgestelde perioden. Meestal zullen dat cijfers zijn op maandbasis (of wellicht op week- of dagbasis). Met die gegevens kun je s_m berekenen. Die kun je dus niet zomaar gebruiken om de veiligheidsvoorraad te berekenen, want die bereken je voor de onzekerheid gedurende de leadtime. En die zal in veel gevallen anders zijn dan precies de periode uit de administratie (de maand) waarop je s_m is gebaseerd. Je moet een correctie aanbrengen om de standaarddeviatie van de vraag over de onzekere periode te bepalen.

De lengte van de onzekere periode is bij bestelsystemen met variabele besteltijdstippen gelijk aan de leadtime, maar bij de s-bestelsystemen komt er nog wat bij.

De standaarddeviatie van de vraag gedurende de leadtime s_L, kun je afleiden uit de standaarddeviatie s_m die je uit administratieve gegevens haalt, met de hierboven uitgelegde formule:

σ_L = σ_m x √L

Hierin staat L voor de leadtime. Let erop dat je voor L dezelfde tijdseenheid gebruikt als voor σ. Dus: bijvoorbeeld beide in weken of beide in maanden.

Met de formule herleid je de spreiding s_m (die bijvoorbeeld berekend is voor periodes van één maand) naar de spreiding over een kortere of langere levertijd. Bijvoorbeeld:

1 maand:           σ_m x √1           = σ_m stuks

2 maanden:       σ_m x √2           = σ_m x 1,4 stuks

½ maand:           σ_m ´x√0,5        = σ_m x 0,7 stuks

1 week : σ_m x √0,25       = σ_m x 0,5 stuks (als 1 maand = 4 weken)

 

Omdat je meestal zult werken met een s die is gebaseerd op vaste periodes (uit de administratie), zullen we de formule voor de veiligheidsvoorraad gaan aanpassen aan de periode waarop de onzekerheid betrekking heeft:

• een B-bestelsysteem de levertijd L
• een s-bestelsysteem de levertijd L plus het bestelinterval i.

Voor een B-systeem wordt de formule voor de veiligheidsvoorraad als volgt:

vv = κ x σ x √L

Voor een s-systeem komt daar het bestelinterval als onzekerheidsperiode bij:

vv = κ x σ x √(L+i)

Hierin is:

k = veiligheidsfactor

s = de standaard deviatie per standaard periode

L = leadtime

i  = bestelinterval

 

De complete formules voor de bestelniveaus ‘B’ of ‘s’ worden als volgt:

B = d x L + vv               =          d x L + κ x σ x √L

s = d x (L+i) + vv          =          d x (L + i) + κ x σ x√(L+i)

Waarin:

L = de gemiddelde levertijd

d = de te verwachten gemiddelde afname per tijdseenheid

s = standaarddeviatie

k = veiligheidsfactor

i = bestelinterval

In de tabel (bijlage 1) en ook in figuur 9 kun je aflezen dat de kans op nee-verkoop niet evenredig afneemt, als je de veiligheidsvoorraad steeds met een vaste hoeveelheid laat toenemen. Dus ook je servicegraad stijgt niet evenredig met een verhoging van je veiligheidsvoorraad.

Is een veiligheidsvoorraad ter grootte van 3 x σ in plaats van 2 x σ beter of minder goed? Weegt de relatief grote toename van je voorraadkosten op tegen de beperkte verbetering van de servicegraad? Dezelfde vraag kun je jezelf stellen over een veiligheidsvoorraad van 2σ in plaats van 1σ.

Bij elk stapje naar rechts langs de vraagverdeling, krijg je een steeds kleinere toename van je servicegraad. Of omgekeerd, elke extra procent minder nee-verkoop bereik je met onevenredig veel meer veiligheidsvoorraad. Je voorraadkosten nemen dus explosief toe als je steeds hogere service-eisen gaat stellen. In de praktijk zul je de veiligheidsvoorraad niet heel erg groot kiezen. Je bent gedwongen om een zeker risico van nee-verkoop te accepteren. Dat speelt natuurlijk vooral een grote rol, bij producten met lange leadtimes.

We hebben je laten zien, dat je veiligheidsvoorraden kunt uitrekenen met behulp van overschrijdingskansen. In de praktijk zie je nog al eens dat er gewerkt wordt met andere methoden om een veiligheidsvoorraad vast te stellen. Bijvoorbeeld:

• een vaste hoeveelheid (bijvoorbeeld altijd 25 stuks),
• een percentage van de jaarafzet (bijvoorbeeld een veiligheidsvoorraad van 5% van de jaaromzet),
• een aantal malen de gemiddelde vraag per tijdseenheid (bijvoorbeeld een veiligheidsvoorraad van 2 weken).

Helaas, deze manieren van ‘rekenen’ aan een veiligheidsvoorraad hebben geen enkele wetenschappelijke of statistische onderbouwing, het is niets anders dan een willekeurige beslissing. Op gevoel, in plaats van op feiten.

Veiligheidsvoorraad is bedoeld voor het zo goed mogelijk opvangen van de onzekerheid over eventuele pieken in de vraag en behoort daarom gebaseerd te zijn op de leadtime en de spreiding van de vraag gedurende de leadtime, niet op de gemiddelde vraag of op een vage redenering.