Logicollege

In de praktijk zul je vaak zien dat de vraag gedurende de leadtime varieert, terwijl de leadtime zelf ook niet constant is. In zo’n geval moet je veiligheidsvoorraad groot genoeg zijn voor het opvangen van beide onzekerheden. De daarvoor benodigde veiligheidsgraad zou je kunnen bepalen door de uitkomsten van de formules voor beide onzekerheden te combineren door optellen van de veiligheidsvoorraad voor de vraagvariatie en die voor de levertijdvariatie. Dat levert echter een te grote veiligheidsvoorraad op.

Dat zit hem in de kansverdelingen. Het kan best zijn dat de vraag veel groter is dan gemiddeld, maar het zou wel erg toevallig zijn als dan ook de levertijd veel langer dan gemiddeld uitpakt. Dat kan wel, maar de kans op die combinatie is klein.

Als het gaat om twee grootheden die onafhankelijk van elkaar variëren, dan mag je de afzonderlijke varianties optellen en uit de gevonden som de wortel te trekken om de gecombineerde spreiding berekenen (even ter herinnering: de variantie is het kwadraat van de standaarddeviatie).

In formulevorm:

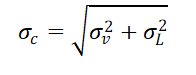
Hierin is σ_c de gecombineerde spreiding en zijn σ_v en σ_L de spreidingen in onafhankelijke grootheden, in dit geval de vraag en de levertijd. Let op, ze moeten wel in dezelfde eenheid zijn uitgedrukt, bijvoorbeeld allebei in stuks per maand.

Als je de gecombineerde spreiding toepast voor bepalen van de veiligheidsvoorraad, dan moet je er dus voor zorgen, dat σ_V en σ_LT in dezelfde eenheid worden uitgedrukt, bijvoorbeeld allebei als de spreiding van het aantal stuks gedurende de levertijd.

Als de leadtime afwijkt van de eenheid van de spreiding, zul je dus eerst de spreiding van de vraag gedurende de leadtime moeten bepalen.

De spreiding van de vraag per maand herleid naar de spreiding gedurende de leadtime
σ_v = σ_M x √L     de variantie is σ²_M x L    

De spreiding van de vraag per maand herleid naar de spreiding van de leadtime

σ_LT = σ_L x d    de variantie is σ²_L x d²

De gecombineerde standaarddeviatie is de wortel uit de som van de varianties:

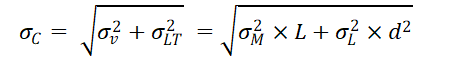
De benodigde veiligheidsvoorraad vind je door σ_C te vermenigvuldigen met de veiligheidsfactor k die behoort bij de gewenste servicegraad. Dat resulteert in de volgende formule voor de gecombineerde veiligheidsvoorraad voor het afdekken van de onzekerheid in de vraag èn in de levertijd:

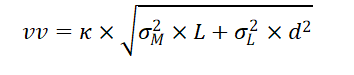
Voorbeeld

De vraag naar koffie in supermarkt SuperM blijkt ongeveer normaal verdeeld te zijn, met een gemiddelde van 60 pondspakken per dag met een standaardafwijking van 15 pakken. De leadtime voor aanvulling van de voorraad is (bij benadering) ook normaal verdeeld. De gemiddelde levertijd bedraagt 3 dagen, met een standaardafwijking van 0,5 dag. Bij welke voorraad moet er worden besteld als SuperM voor koffie streeft naar een servicegraad van 98%?

Het bestelniveau is gelijk aan de gemiddelde vraag gedurende levertijd (3 x 60) plus de veiligheidsvoorraad. Voor de veiligheidsvoorraad vult SuperM de formule in:

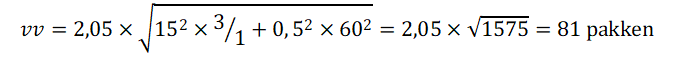
Het bestelniveau is wordt (bij een BQ-systeem) 3 x 60 + 81 = 261 pakken.

Tenslotte:

• Aan de redenering moeten we volledigheidshalve nog toevoegen, dat het vaak zal voorkomen dat variatie in vraag en variatie in levertijd toch enigszins van elkaar afhankelijk zijn. Als de consumentenvraag naar een bepaald product opeens stijgt, is de kans groot, dat de producent van dat product niet aan alle detailhandelsbedrijven op tijd kan leveren. Een detaillist krijgt in deze situatie te maken met stijging van de vraag en tegelijk met een langere levertijd. In deze situatie is sprake van wederzijdse afhankelijkheid van de variatie in vraag en in levertijd. Om ook in deze situatie de servicegraad op peil te houden met veiligheidsvoorraad, zou een aanvulling op bovenstaande formule nodig zijn. In de praktijk zul je dit liever niet structureel in je bestelsysteem willen verwerken, omdat het gaat om voor iedereen duidelijke incidenten. De invloed daarvan zul je niet blijvend willen vertalen in veiligheidsvoorraad en dus in voorraadkosten.

• De veiligheidsvoorraad is bedoeld voor het opvangen van toevallige variaties in vraag en levertijd, bij verder gelijkblijvende condities in de markt en in de levervoorwaarden.
  De veiligheidsvoorraad is niet bedoeld voor het opvangen van structurele vraagverhoging of verlaging en ook niet voor structurele aanpassing van de leadtime.

• Wil je dat je veiligheidsvoorraad meebeweegt als er een trend (omhoog of omlaag) is in de vraag, doe dat dan door in de formules op de plaats van de historisch gemiddelde vraag gedurende de leadtime (d) te rekenen met de prognose van de vraag (herleid naar de leadtime).

• De verdeling van de levertijd lijkt meestal niet goed op een normale verdeling. Het is meestal een scheve verdeling, een Poissonverdeling of bij korte levertijden een negatief exponentiële verdeling.

figuur 10: drie soorten kansverdeling