Leerdoelen
In deze module leer je hoe je met behulp van de standaard spreiding kunt berekenen hoeveel veiligheidsvoorraad je nodig hebt. Daarbij leer je onderscheid te maken tussen normaal-verdeelde vraag en Poissonverdeelde vraag.
Tenslotte leer je hoe je de servicegraad kunt berekenen van een assortiment, bijvoorbeeld van een grondstoffenmagazijn.
Inleiding
Zoals je in Module 6 leerde, is veiligheidsvoorraad bedoeld voor het opvangen van variatie in de onafhankelijke vraag gedurende de levertijd, of voor opvang van variatie in de levertijd. Veiligheidsvoorraad heb je nodig om de kans te verkleinen dat je voorraad onvoldoende is om de gehele levertijd te overbruggen.
We gebruiken het begrip kansverdeling om met kansen te kunnen rekenen. Dat vraagt om toelichting. Een kansverdeling is een curve die aangeeft hoe groot de kans is op een bepaalde waarde van een verschijnsel. Bijvoorbeeld hoe groot de kans is dat een willekeurig persoon die je gaat ontmoeten langer is dan 1,88m. Onder de kansverdeling van de vraag verstaan we de curve die aangeeft hoe groot de kans is dat klanten gedurende een bepaalde periode een bepaalde hoeveelheid afnemen. Omdat alle waarden (in theorie) kunnen optreden, verdelen we de frequentie van optreden van ‘het’ verschijnsel meestal in klassen. Bijvoorbeeld het aantal mannen met een lengte 1,70m tot 1,75m, 1,75m tot 1,80m, 1,80m tot 1,85m enzovoorts. Als je van alle mannen (die je kent) een streepje te zetten bij hun lengteklasse krijg je een frequentieverdeling. Die kun je in een grafiek weergeven, maar ook in een tabel uitzetten. Dan noemen we het een frequentietabel. Je hebt dan een hulpmiddel om een goede schatting te maken van de willekeurige persoon die je gaat ontmoeten: die lengte zal waarschijnlijk in de buurt van het gemiddelde zijn en met grote zekerheid tussen de grootse en kleinste klasse van je turflijstje.
Voorbeeld
Kollor meet de viscositeit van de verf voordat deze de fabriek verlaat. Uit de meting moet blijken dat de viscositeit minder dan 10% afwijkt t.o.v. de normwaarde. Uit registratie blijkt dat de kleinste afwijking nul was en de grootste 9%. Deze uitersten komen echter niet vaak voor. Charges met 3 of 4% afwijking komen vaker voor. Van de 1000 geregistreerde charges is een frequentietabel gemaakt door per afwijkingspercentage te tellen in hoeveel charges die afwijking is voorgekomen. Let op, Kollor rondt de afwijkingen dus af op hele procenten. In werkelijkheid kunnen de percentages elke waarde hebben, wat wil zeggen dat de klasse van 3% bijvoorbeeld aangeeft, hoe vaak een viscositeitsafwijking voor kwam die groter was dan 2,5% en kleiner of gelijk aan 3,5%.
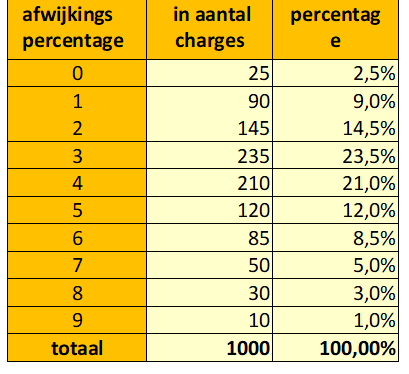
tabel 1: frequentieverdeling van viscositeitsafwijking per charge
De kans dat een bepaalde gebeurtenis zich voordoet heeft steeds een bepaalde waarde. Bijvoorbeeld de kans dat je een charge treft waarin de viscositeit 5% afwijkt van de norm, is 12% volgens de waarnemingen bij Kollor. Omdat de charges elkaar in principe niet beïnvloeden, zijn deze kansen onafhankelijk van de vorige charge en dus onafhankelijk van elkaar. Als we de tabel in een staafdiagram omzetten, ontstaat het volgende beeld (figuur 1).
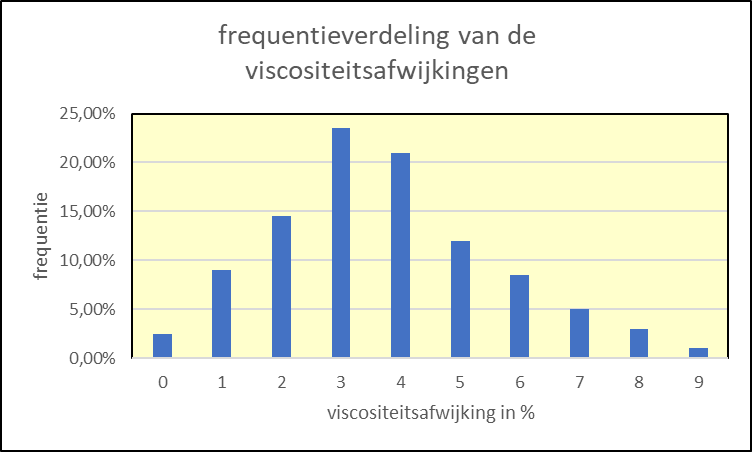
figuur 1: frequentieverdeling afwijking per charge
Als je de verdeling zou weten van de afzet per maand van een bepaald artikel, zou je daarmee de kans kunnen inschatten, hoeveel je in een bepaalde periode van dat artikel zult verkopen.
Logistiek manager John-Peter van Kollor laat alle beschikbare gegevens over de afzet per maand van scheepscoating uit de administratie halen en stelt er een frequentieverdeling van op.
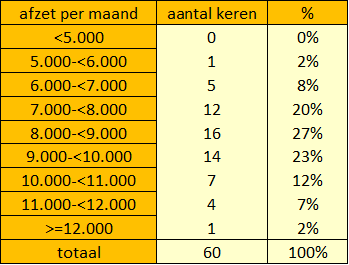
tabel 2: frequentieverdeling van de afzet per maand van scheepscoating
Vervolgens zet John-Peter de getallen uit in een grafiek. Hij krijgt dan de kolommengrafiek van figuur 2.
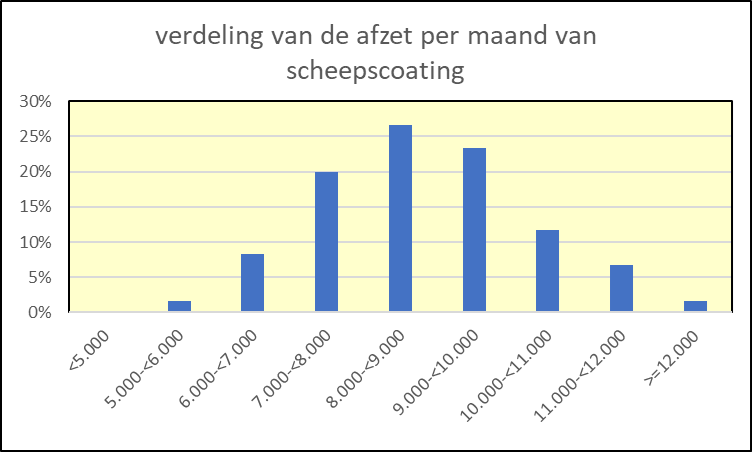
figuur 2: frequentieverdeling van de maandelijkse afzet van scheepscoating
Hij ziet in de grafiek en in tabel 2 dat de afzet zich concentreert rond een gemiddelde van 8.000 á 9.000 eenheden, met een zekere spreiding daaromheen.
Heel vaak zal de afzet van artikelen, zo ongeveer verdeeld zijn zoals geschetst in figuur 2. Tenminste als het een artikel met een onafhankelijke en niet al te lage gemiddelde afzet betreft. Als je de toppen van de kolommen met elkaar zou verbinden, blijkt dat deze afzetverdeling tamelijk goed overeenkomt met de vanuit de statistiek bekende klokvorm van de normale verdeling.
