Logicollege

Leerdoelen

In deze Module leer je de economische achtergronden kennen waar het EOQ-model op  is gebaseerd.

Je leert hoe je het model kunt gebruiken voor korte en voor lange termijn vraagstukken, hoe je rekening kunt houden met de productiesnelheid en met de waardestijging van het product tijdens het fabricageproces. Je leert hoe het model kan worden toegepast bij verschillende soorten kortingen op de inkoopprijs en bij een seizoenpatroon in de vraag.

Bij JIT speelt voorraad een heel andere rol, dan is de optimale serie gelijk aan 1. Wat dat betekent voor het EOQ-model leer je in deze module. Tenslotte leer je hoe je met tijdgefaseerd bestellen kunt inspelen op de vraag.

Inleiding

We beginnen met een voorbeeld van een bestelling, waarbij te bestellen hoeveelheid nog niet vaststaat. Voor het bestellen is een seriegrootte bepaling nodig. Daarbij is de wens, dat de kosten zo laag mogelijk zullen zijn. Na omschrijving van de situatie, gaan we in het voorbeeld op zoek naar de oplossing door in een tabel een flink aantal mogelijkheden op een rijtje te zetten om op zoek te gaan naar de serie met de laagste kosten.

Voorbeeld

Verffabriek Kollor verbruikt per jaar 800 stuks van een bepaald fabricage-hulpmiddel. De inkoopprijs van dit item is € 25,-per stuk. Het verbruik van het artikel is gelijkmatig en blijft constant.

Nelly, de assistent inkoper van Kollor, heeft uitgezocht dat de kosten om één exemplaar van het artikel een jaar in voorraad te houden 20% van de inkoopprijs bedragen, dat wil zeggen € 5,- per jaar. Daarnaast weet ze, dat het plaatsen van een bestelling geld kost. Navraag bij de controller leert, dat het plaatsen van elke bestelling Kollor € 75,- kost. Die kosten bestaan uit haar tijd, de afwikkeling van de goederenontvangst, de kwaliteitskeuring en de factuurcontrole. Voor haar eigen gemak zou ze ervoor kunnen kiezen om de benodigde 800 stuks voor een jaar allemaal tegelijk te bestellen, maar ze kan de totale jaarbehoefte ook in kleinere delen (in series) bestellen, waardoor de voorraad lager zal zijn. H

Nelly begrijpt dat haar bestelgrootte belangrijke gevolgen heeft voor de kosten van Kollor. Ze vindt het een interessant probleem en bedenkt een manier om uit te vinden wat de hoeveelheid is waar de kosten het laagst bij zullen zijn. Voor een aantal verschillende seriegroottes berekent Nelly de kosten. Die kun je zien in tabel 1.

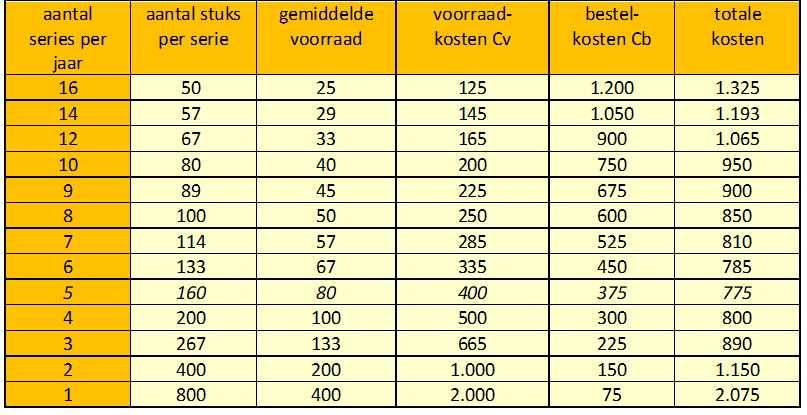
tabel 1: kosten per serie

Nelly ontdekt dat bij 5 series van 160 stuks, per jaar de totale kosten (C_tot) het laagst zijn. Als Nelly haar berekening controleert met de formule van Camp, blijkt het aantal van 160 stuks per serie dicht in de buurt te zitten van de volgens Camp optimale seriegrootte.

Als we de gegevens uit tabel 1 in grafiekvorm weergeven, dan krijgen we

figuur 1.

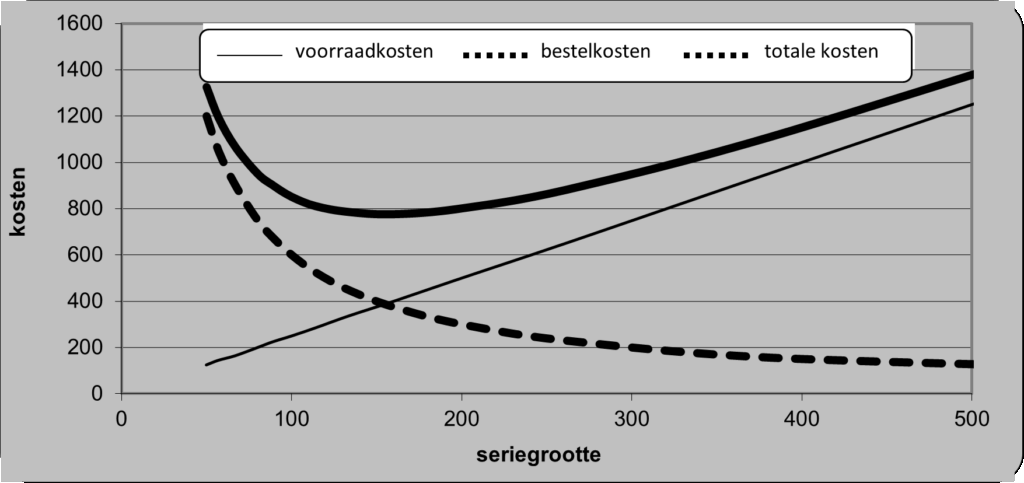
figuur 1: totale kosten als functie van de seriegrootte Q, gebaseerd op de gegevens in tabel 1

In de grafiek kun je zien dat de totale kosten bij een Q van circa 160 stuks het laagst zijn. Als je een nauwkeurigere waarde voor het optimum wil, dan kun je die vinden door meer regels in de tabel in te voegen, zodat de tussenstapjes kleiner worden. Je kunt natuurlijk ook de formule van Camp gebruiken.