Logicollege

De optimale seriegrootte kun je ook in één keer berekenen met de formule van Camp, waardoor je het tijdrovende invullen van een tabel kunt vermijden. Die formule zullen we gaan afleiden, maar daarvoor gaan we eerst de verschillende variabelen die een rol in het model spelen, van een symbolische naam voorzien:

Q    = grootte van de bestelserie,

D     = de te verwachten jaarlijkse vraag,

F     = order- of bestelkosten per bestelling,

a    = factor voor de voorraadkosten per jaar,

K     = kostprijs per eenheid product,

C_tot   = totaal van de voorraad-en bestelkosten.

voorraadkosten

We beginnen met het uitdrukken van de jaarlijkse voorraadkosten in een formule, zodat je voor een gegeven product bij elke waarde van Q kunt berekenen wat de bijbehorende voorraadkosten zijn. Voor de voorraadkosten nemen we alleen de seriegrootte voorraad mee in de berekening. Er zal waarschijnlijk in de praktijk ook veiligheidsvoorraad zijn, maar die heeft geen relatie met de kosten die ontstaan door de seriegrootte. Veiligheidsvoorraden en de kosten daarvan hebben geen invloed op de optimale seriegrootte, we laten ze dus buiten ons model.

De factor voor de voorraadkosten α bestaat uit de 3 R-en: rente, ruimte en risico.

Wat je moet gebruiken als waarde voor die posten hangt af van de situatie van je onderneming.  We leggen dat uit.

Voor de post ‘rente’ kun je rekenen met de rente die de bank vraagt voor een lening, maar beter is wellicht om te rekenen met de (gemiddelde) rentabiliteit van het eigen vermogen. Te vinden in de jaarcijfers van de onderneming. Je bedrijf kan het geld maar één keer gebruiken, voor voorraad, voor het dekken van de kosten of voor het investeren in vernieuwing of uitbreiding, dus: als geld schaars is, moet je rekenen met een hoge ‘rente’. Als er voldoende geld (of bankkrediet) beschikbaar is, reken je met de bankrente.

Voor de post ‘ruimte’ geldt in grote lijnen eenzelfde redenering als voor de ‘rente’. Als er ruimte genoeg beschikbaar is, kun je de ruimtekosten buiten beschouwing laten, maar meestal is dat niet zo. Dan kun je beter rekenen met de m² prijs in het huurcontract (of bij een eigen pand met een berekende prijs (gebaseerd op afschrijving en onderhoud). Is de ruimte erg krap, reken dan met de kosten voor externe opslag. De post ‘ruimte’ loopt in de praktijk niet precies lineair met de voorraadhoogte op. In gebruik nemen van ruimte gaat immers in stappen. Een palletplaats blijft even groot, of er nu 1 of 100 stuks op de pallet liggen. Ruimte uitbreiden gaat niet per m², maar met hele hallen etc. Als je beschikbare ruimte helemaal vol zit en je voor één extra product een hele hal moet bijbouwen, moet je dan de kosten van die hele hal toerekenen aan dat ene product? Gemakshalve nemen we in het model een vaste factor van de kostprijs van een eenheid product voor de ruimtekosten. De redenering bij het bepalen van die waarde is: neem 0 als je ruimte genoeg hebt, reken een marktconforme  huurprijs per m² als je krap in de ruimte zit.
Vergeet tenslotte niet, om die kosten per m² te delen door het de waarde van aantal eenheden dat je op een m₂ kunt opslaan om daarmee de factor ‘ruimtekosten’ te bepalen.

Het ‘risico van voorraad’ bestaat op zich uit een aantal factoren. Bijvoorbeeld brandschade en waterschade. Dit risico is te verzekeren, dus de premie valt onder de risico-kosten. Maar er speelt meer. Er kan door allerlei oorzaken iets ‘verdwijnen’, iets breken of onbruikbaar worden. Dat is onverzekerbaar. Het hangt af van de situatie of dit een substantieel van de voorraadkosten is en speelt vooral een rol bij kleine kostbare producten, bij breukgevoelige producten en bij producten die geconditioneerd moeten worden bewaard. En er speelt bij voorraad het probleem van ‘veroudering’, met op zich weer een aantal subproblemen. Bijvoorbeeld bij levensmiddelen staat op de verpakking een houdbaarheids- of best before datum. Daarna niet meer te verkopen, niks meer waard. Bijvoorbeeld in de mode, of bij computercomponenten volgen de generaties van het product snel op elkaar. De ‘oude’ uitvoering daalt enorm in prijs als een ‘nieuwe’ op de markt komt. Soms is de ‘oude’ zelfs onverkoopbaar. Het risico stijgt met grotere voorraad, dus met grotere series. Wellicht kun je in de jaarrekening terugvinden hoeveel er is afgeschreven op voorraad. Let op, dat is dan waarschijnlijk inclusief de afschrijving ten gevolge van ‘verdwijnen’.

Deel de verzekeringspremie en de afschrijving door de kostprijswaarde van de omzet om de factor te vinden voor het EOQ-model. In de praktijk (buiten juwelen, de mode en de snel ontwikkelende technologie) vormen de risico-kosten vaak maar een klein deel van de R-en.

Voor de voorraadkosten per eenheid product nemen we in ons model de drie R-en samen in de factor α, dus in een percentage van de kostprijs. Vermenigvuldigd met de kostprijs (K) van het betreffende product levert dat als voorraadkosten: a x K per jaar. (Let op, als α een getal in procenten is, dan moet je dat getal nog door 100 delen voor je het kunt invullen in de formule)

• De gemiddelde voorraad in stuks is in ons model (afgezien van eventuele veiligheidsvoorraad) gelijk aan de halve seriegrootte: ½ Q.
  De waarde daarvan is:  ½ Q x K
• De totale voorraadkosten per jaar zijn dan in formulevorm weer te geven met
  C_v = ½Q x a x K.

order – of bestelkosten

Vervolgens drukken we de jaarlijkse order- of bestelkosten uit in een formule. Zodat we voor elke willekeurige waarde van Q kunnen berekenen wat de bijbehorende bestelkosten zijn.

De kosten die je per bestelling maakt, noemen we F.

F bestaat uit de kosten die ontstaan als je (extern) bij een leverancier bestelt of de kosten die intern ontstaan door het omstellen in de productie. In F zitten bijvoorbeeld de verwerkingskosten van de leverancier, de transportkosten, de kosten van ontvangst- en kwaliteitscontrole en van intern transport en van fysiek en administratief in voorraad nemen. Als je het model wil gebruiken voor het berekenen van de optimale productieserie, dan omvat F bijvoorbeeld de kosten voor schoonmaken, omstellen en inlopen van de installatie en de kosten van het interne transport naar de opslag. Die kosten bestaan voornamelijk uit personeelskosten (arbeidsuren) en voor een deel uit verloren gegaan materiaal tijdens het inlopen. Als de installatie de bottleneck is, wordt F een stuk groter, want een uur niet gewerkt op een bottleneck, is en uur verloren aan omzet. Bij de omstelkosten moet je de gederfde winst tellen, de winst die had kunnen worden gemaakt, als de bottleneck had kunnen doorwerken.

Per jaar is het aantal bestellingen (of het aantal productieorders als het gaat om fabricage) gelijk aan het totale jaarverbruik, gedeeld door de seriegrootte: D/Q.

De orderkosten per jaar zijn gelijk aan het aantal bestellingen, maal de kosten per bestelling:

C_b = (D/Q) x F

totale kosten

De totale kosten, althans voor zover die relevant zijn voor het vraagstuk van de seriegrootte, vind je door het optellen van de voorraadkosten en de bestelkosten.

De totale kosten C_tot zijn:

of, anders geschreven:

minimale kosten

Het minimum van de totale kosten kun je wiskundig vinden door de kostenfunctie naar Q te differentiëren en daarna de afgeleide functie gelijk aan nul te stellen.

Differentiëren naar Q van de bovenstaande totale kostenfunctie C levert:

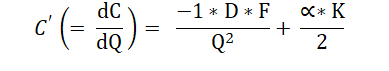
Door deze afgeleide functie op nul te stellen krijg je:

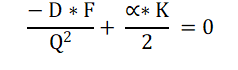
De (negatieve) eerste term brengen we naar de rechterkant van het = teken (en wordt dan positief):

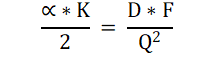
Beide zijden van het = teken vermenigvuldigen met Q² en met 2 levert:

Beide zijden delen door αK:

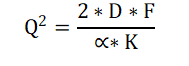
Aan beide zijden de wortel trekken levert de formule voor het berekenen van de waarde van Q die behoort bij het minimum van de totale kosten. De formule van Camp:

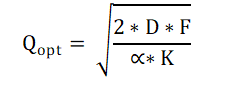
In dit speciale geval (de combinatie van een continu dalende hyperbool en een continu stijgende rechte lijn) ligt het minimum van de totale kosten op het punt, waar de voorraadkosten gelijk zijn aan de bestelkosten.

In de formule is Q_opt de optimale of economische seriegrootte is. Deze wordt ook wel aangeduid met Q* en vaak de EOQ genoemd (Economic Order Quantity).

Als je de formule van Camp gaat toepassen op het in tabel 1 . gegeven bedrijfsvoorbeeld, met D = 800, F = 75, α = 0,20 en K = 25, dan krijg je het volgende resultaat:

De schatting die we in het voorbeeld in de Inleiding van deze module maakten (met de tabel) blijkt aardig in de buurt te komen van de echt optimale seriegrootte.