Logicollege

Het klokvormige verloop van een normale verdeling (Gauss-kromme) laten we zien in figuur 1. De top van de grafiek staat boven het gemiddelde ‘nul’ (mu, μ = 0). De grafiek is gemaakt voor een standaardafwijking van 1 (sigma, σ = 1). In deze vorm heet het de ‘standaard normale verdeling’. Daar kun je elke andere normale verdeling uit afleiden.

Je moet de grafiek als volgt lezen:

• De curve is symmetrisch, aan beide kanten van het gemiddelde verloopt de grafiek gelijk.
• Bij elke waarde op de x-as kun in de grafiek de bijbehorende kansdichtheid Het is de afstand van dat punt op de x-as tot aan de kromme (loodrecht verticaal gemeten).
• Het hoogste punt van de grafiek is in het midden (bij de standaard verdeling dus precies boven X=0). Je kunt daaruit afleiden, dat hier de kansdichtheid het groots is. In en rond het midden is de kansdichtheid veel groter, dan in de ‘buitengebieden’.
• De kans dat X zich bevindt tussen twee waarden, is gelijk aan het oppervlak van de grafiek, dat door die twee waarden wordt omsloten.
• De kans op een waarde van X die groter is dan nul (dus alles rechts van het midden), is even groot als de kans op een waarde van X die kleiner dan het midden. Beide zijn 50%
• Het oppervlak onder de grafiek, rechts van een bepaalde waarde van X, geeft de kans aan dat die waarde of een grotere waarde zich kan voordoen. Dit heet de overschrijdingskans of ook wel de rechter overschrijdingskans.
• Het oppervlak links van een bepaalde waarde van X geeft de kans aan dat die waarde of een kleinere waarde zich voordoet. Dit is de onderschrijdingskans, of ook wel de linker overschrijdingskans.
• Hoe hoger de top in het midden van de grafiek (dus hoe steiler de grafiek links en rechts van het midden verloopt), hoe meer kans dat zich een waarde in de buurt van het gemiddelde voordoet. De standaard spreiding is dan klein.
• Hoe breder (en platter) de grafiek, hoe groter de spreiding is, hoe meer kans op een waarde ver van het gemiddelde.
•  

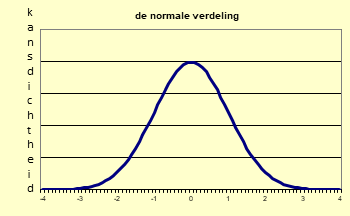
figuur 3: de standaard normale verdeling N(0,1)

In de praktijk zul je meestal uitgaan van een frequentieverdeling in plaats van een continu doorlopende kansverdeling. Als ‘het’ verschijnsel normaal verdeeld is en je heel veel waarnemingen doet en de klassen van de turflijst maar klein genoeg zijn, zal de frequentieverdeling de vorm heel dicht benaderen van de Gauss-klok. Zie figuur 4, waarin we met een klassebreedte van 0,1 (dus 0,1 x sigma) de geturfde kansdichtheid en tonen van een verschijnsel dat normaal is verdeeld. Figuur 5 is een weergave van de onderschrijdingskans (ook wel genoemd de linker overschrijdingskans).

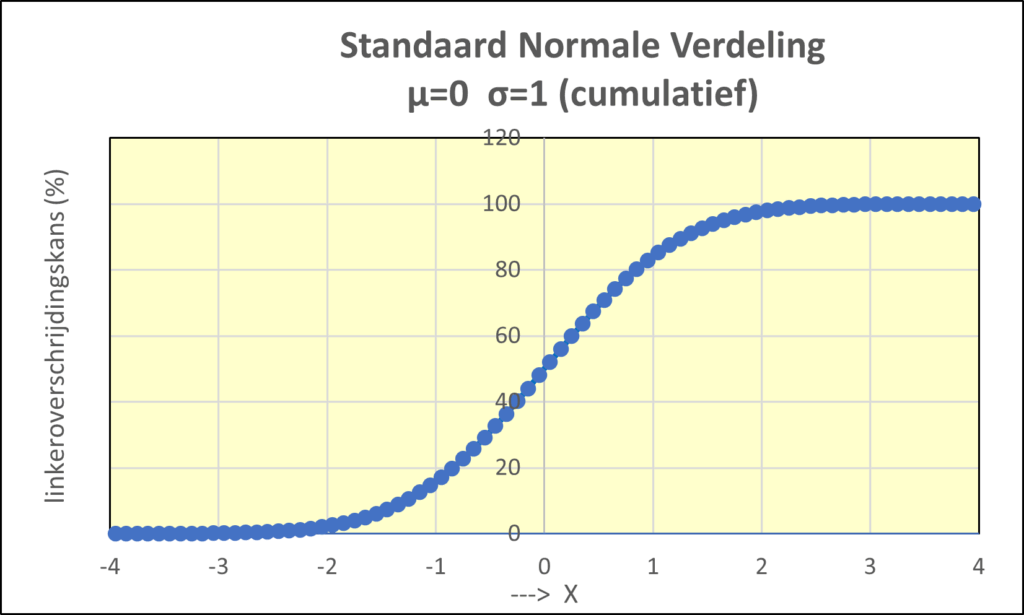
Figuur 4: Kansverdeling van N(0,1);                                 Figuur 5: Onderschrijdingskans geturfd met klassen van 0,1 breed

Het gemiddelde is meestal niet 0, zoals in de standaard normale verdeling. De normale (kans)verdelingen hebben wel altijd een klokvorm. Maar de ene grafiek is wat platter dan de standaard en de ander verloopt wat steiler. Een platte grafiek betekent een grote spreiding rondom het gemiddelde, een steile grafiek duidt op een kleine spreiding.

Uit bovenstaande grafiek kun je afleiden dat naarmate een waarde van X verder van het gemiddelde af ligt, de kans dat die waarde werkelijk optreedt steeds kleiner wordt. Maar hoe ver ook vanaf het gemiddelde, de kans wordt (theoretisch) nooit nul. De kromme raakt de x-as niet, maar loopt er asymptotisch naar toe. Dit betekent dat er in theorie altijd wel een kans is op een zeer grote of een zeer kleine waarde, maar dat deze kans niet waarschijnlijk is en in de praktijk dus niet zal voorkomen.

De figuren 1, 3 en 4 laten de kansdichtheid zien. De kansdichtheid van een verdeling laat zien hoe de waarschijnlijkheid over de mogelijke waarden (van X, de stochastische variabele) is verdeeld. Het is alleen mogelijk om een kans toe te kennen aan een aaneengesloten deel van de X-as