Logicollege

We noemden het al aan het eind van Hoofdstuk 1: het is alleen mogelijk om een kans toe te kennen aan een aaneengesloten deel van de X-as. We werken dat verder uit en beginnen met de kans dat een bepaalde waarde van x wordt overschreden, dat de excentriciteit van x wordt overschreden. Excentriciteit, want als die waarde van x nul zou zijn, dan weet je al dat de kans op overschrijding 50% is. Het gaat erom wat te doen als de betreffende waarde van x anders is dan 0.

De kans dat een zekere excentriciteit wordt overschreden, is voor iedere normale verdeling met een vaste formulering uit te drukken. Bijvoorbeeld: de kans op het optreden van een waarde groter dan het gemiddelde (μ) plus de standaarddeviatie (s) is voor iedere normale verdeling altijd gelijk aan 15,87%. Dit heet de overschrijdingskans van μ + σ en die is bij elke normale verdeling dus 15,87%.

Omgekeerd is de onderschrijdingskans van het gemiddelde plus s dus gelijk aan 100% – 15,87% = 84,13%. De onderschrijdingskans van μ + σ is bij elke normale verdeling dus 84,13% en dat is door de symmetrie dan ook weer gelijk aan de overschrijdingskans van μ – σ.

De afstand die een bepaalde waarde (x) van het gemiddelde af ligt, noemen we de excentriciteit. Die excentriciteit drukken we uit in een factor maal σ. De excenticiteitsfactor heeft als symbool kappa, k.

Bij een overschrijdingskans van 15,87% is k dus 1. Bij k = 3 is de overschrijdingskans nog maar 0,13%.

De bij een excentriciteit ‘k’ behorende overschrijdingskans is in een standaardtabel vastgelegd (zie bijlage 1). Je kunt de waardes zelf ook berekenen in Excel. Tik maar in een willekeurige cel:

Je krijgt dan de waarde 84,13%, de formule geeft de onderschrijdingskans bij de excentriciteit waarvan de waarde tussen de haakjes staat. In dit geval dus bij k = 1, dat is dus bij de X-waarde 1 x σ. De overschrijdingskans is 100 – 84,13 = 15,87%

In de praktijk zul je weinig tegenkomen dat de standaarddeviatie van je getallenreeks precies gelijk aan 1 is. Je kunt de kans dat de waarde x₁ wordt overschreden, dan toch met bovenstaande Excel-formule berekenen, maar je hebt wel een correctie nodig: deel de waarde van x₁ door de σ die hoort bij je getallenreeks. De uitkomst vul je in tussen de haakjes in de formule.

Soms wil je niet weten wat de kans is dat een bepaalde waarde wordt overschreden, maar wil je weten wat de kans is op een uitkomst tussen twee waarden, zeg de kans om uit te komen tussen x₁ en x₂. Met behulp van de overschrijdingstabel (of van de Excel-formule) kun je de kans op een uitkomst tussen x₁ en x₂ berekenen, door de overschrijdingskans van x₁ uit te rekenen en daar de overschrijdingskans van x₂ van af te trekken. We laten dat zien in figuur 6. De kans dat X zich zal bevinden tussen de waarden 1,1 en 1,3, wordt aangegeven door de oranje kolom. Het oppervlak (de kans) is te berekenen door de onderschrijdingskans van 1,3, te verminderen met de onderschrijdingskans die hoort bij 1,1. Dat is 0,903 minus 0,864 ofwel 3,9%.

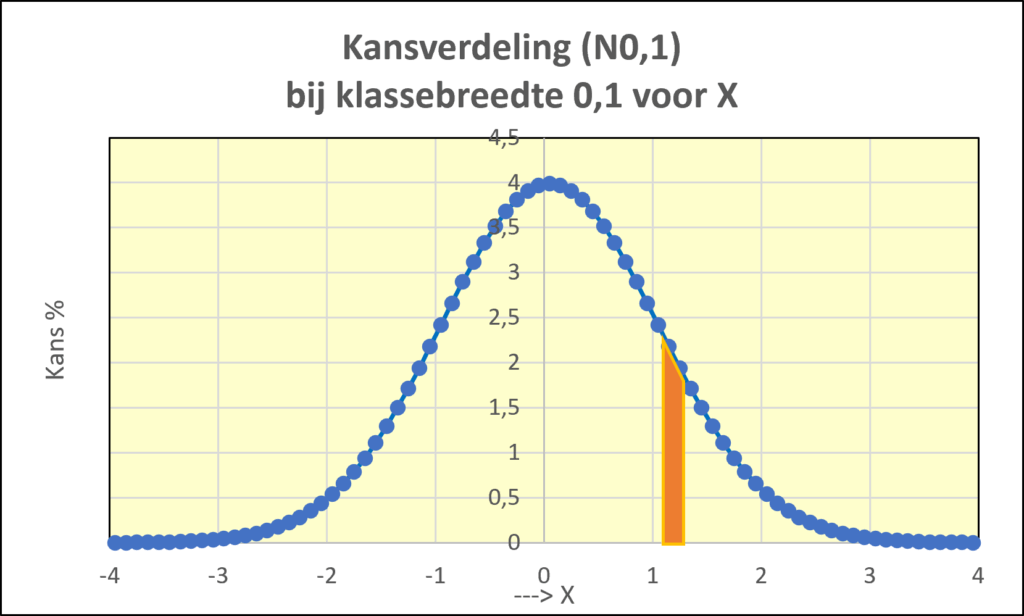
Figuur 6: een kans komt overeen met een stukje oppervlak onder de kromme

Bij het berekenen van de veiligheidsvoorraad zullen we gebruik van gaan maken van de standaarddeviatie. Uit een reeks met historische vraaggegevens berekenen we μ en σ, en voor k kiezen we een waarde die een aanvaardbare overschrijdingskans oplevert. We aanvaarden de kans dat de vraag in een bepaalde periode groter is dan μ + k ´ σ en gaan ervan uit, dat dit de kans is op nee-verkoop. De kans dat we niet uit voorraad kunnen leveren. Bij voorraadbeheer noemen we de excentriciteit k de veiligheidsfactor of de servicefactor.

De tabel van de rechteroverschrijdingskansen van de normale verdeling loopt tot iets meer dan driemaal de standaarddeviatie (3 ´ s), het gebied dat daarbuiten valt, heeft geen praktische waarde voor het voorraadbeheer (zie de figuren 4, 5 en 6). Op een afstand van 3s van het gemiddelde is 99,865% van het oppervlak van de Gauss-kromme afgedekt (volgens bijlage 1 of de Excelberekening = stand.norm.verd(3)).
Met andere woorden, de overschrijdingskans is bij excentriciteit van 3s maar ongeveer 0,13%.

Je kunt nu berekenen, of in de tabel (bijlage 1) aflezen dat:

• Voor de gemiddelde waarde van X de kans op onderschrijdingskans 50% is (k = 0, excentriciteit is nul maal s). Voor voorraadbeheer betekent dit dat als je de vraag in een bepaalde nabije toekomstig periode schat op het in het recente verleden gerealiseerde gemiddelde (μ), de kans 50% is dat de vraag groter zal zijn dan je schatting. En dat ook nog onder de voorwaarde dat er geen plotselinge grote veranderingen in de vraag zullen spelen.
• Bij een excentriciteit van éénmaal s (dus k = 1s) is de kans op overschrijding 15,9%. Stel dat je de vraag voor de nabije toekomst inschat op μ+σ, dan betekent dit er ongeveer 16% kans is dat de vraag groter zal zijn je schatting.
• Bij k = 2s (excentriciteit tweemaal s) is de kans op overschrijding nog maar 2,28%.
• Bij k = 3s is de kans op overschrijding 0,13% en dat is waarschijnlijk verwaarloosbaar als het gaat om voorraadbeheer.