Logicollege

De normale verdeling heeft een klokvormig verloop rond het gemiddelde. De verdeling is symmetrisch. Gemiddelde, modus en mediaan vallen samen. Als je de verdeling tekent van de vraag naar een product, dan wordt je klok aan de linkerzijde afgekapt ter hoogte van de nul, omdat de vraag niet negatief kan zijn. Als het gaat om een product met een hoge gemiddelde vraag, zal je curve nog veel lijken op de klok van de normale verdeling. Maar bij een product met een lage gemiddelde vraag, zal je klok er aan de linkerkant lelijk verminkt uitzien. Als het gemiddelde tamelijk dicht bij nul zit, wordt je grafiek als het ware afgeknipt aan de linkerkant.

In figuur  staan twee normale verdelingen naast elkaar. Nu niet gestandaardiseerd met μ=0 en σ=1, maar met langs de X-as de werkelijke waarden. Stel dat het gaat om verdelingen van de vraag naar product P en product Q. De verdeling van product (P) heeft een gemiddelde vraag van 50 met een standaardafwijking van 5. Het product (Q) lijkt een gemiddelde vraag van 5 te hebben, met eveneens een standaardafwijking van 5. In de figuur is zichtbaar dat Q, door de lage gemiddelde vraag, een relatief hoge kans zou hebben op negatieve vraag. Maar dat kan niet, negatieve vraag bestaat niet (retouren daargelaten). Je kunt uit de figuur afleiden dat voor producten met een kleine gemiddelde vraag de normale verdeling dus geen goede weergave kan zijn van de werkelijke verdeling van de vraag.

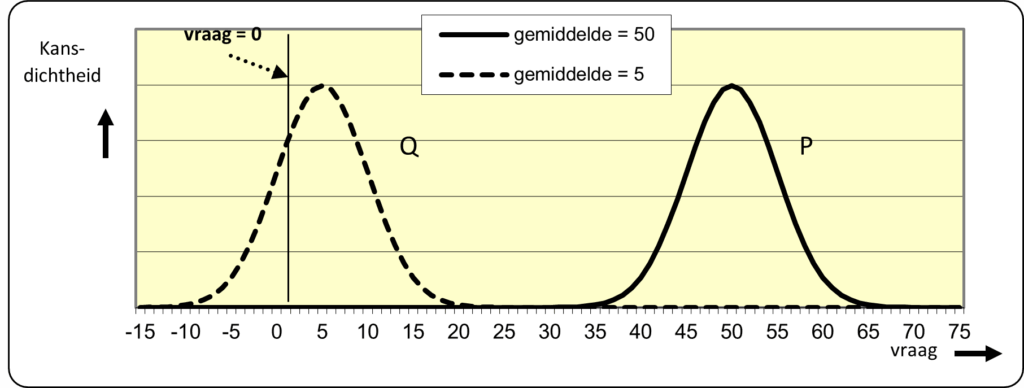
figuur 7: normale verdeling alleen bij hoge gemiddelde vraag

De vraagverdeling van langzaamlopende artikelen kun je beter beschrijven met een andere verdeling dan de normale. Bijvoorbeeld met de Poissonverdeling. Dat is een kansverdeling die in de logistiek veel toepassingen kent. De Poissonverdeling kun je bijvoorbeeld gebruiken voor het berekenen van de kans dat in het komende uur 5 mensen bij een balie aankomen als je weet dat het gemiddelde aantal aankomende klanten 8 per uur is. Bij de Poissonverdeling kunnen geen negatieve getallen voorkomen. En dat komt overeen met de situatie bij de vraag naar artikelen (met name bij artikelen kleine gemiddelde vraag, zoals artikel Q in figuur 7).

In figuur 8 hebben we de Poissonverdeling van een artikel weergegeven met een gemiddelde vraag van 4 stuks per tijdseenheid.

De Poissonverdeling begint links bij nul en is niet symmetrisch. De modus komt niet overeen met het gemiddelde, maar is (per definitie) lager dan het gemiddelde. De standaarddeviatie is bij een Poissonverdeling wat simpeler te berekenen, die is de wortel uit het gemiddelde:

          σ = √μ

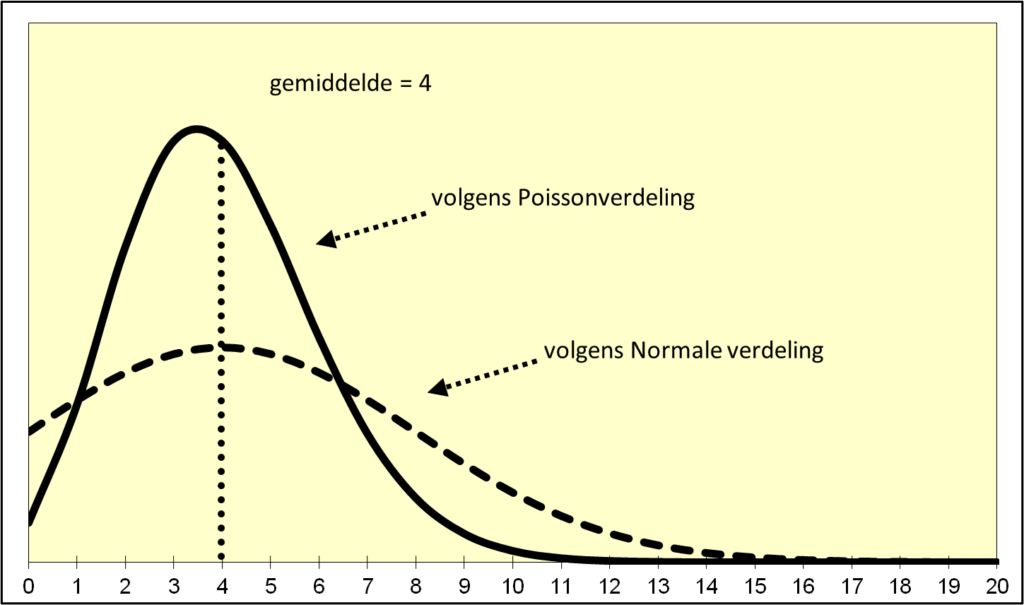
figuur 8: de Poissonverdeling van een langzaam lopend artikel (gemiddelde vraag is 4)

De vraag naar elk artikel is in theorie Poisson verdeeld. Ook als je te maken hebt met een hoge gemiddelde vraag. Omdat we in voorraadbeheer voornamelijk geïnteresseerd zijn in het rechterdeel van de grafiek, kun je vaak de normale verdeling gebruiken als redelijke benadering. We zullen dat ook in deze modulen bij voorkeur doen, omdat rekenen met de normale verdeling eenvoudiger gaat dan met de Poissonverdeling. Ler erop dat je in uitzonderlijke situaties zoals bij zeer lage gemiddelde vraag en/of bij een vraag in horten en stoten (lumpy demand), de normale verdeling niet mag gebruiken, omdat de situatie te veel afwijkt. In deze gevallen kun je beter de Poissonverdeling gebruiken of wellicht de Binomiale verdeling.