Logicollege

Al eerder noemden we de twee centrale vragen van voorraadbeheer: wanneer bestellen en hoeveel bestellen. In deze paragraaf gaat het over de vraag hoeveel je het beste tegelijk kunt bestellen.

De hoeveelheid waarmee je je voorraad aanvult, heeft directe invloed op de voorraad- en de bestelkosten. Als je grotere hoeveelheden tegelijk gaat bestellen, krijg je een hogere gemiddelde voorraad en dus hogere voorraadkosten. Maar als je in kleine series bestelt, moet je vaak bestellen. Dat kost je meer tijd, met hoge bestelkosten als gevolg. Je moeten dus twee kosten tegen elkaar afwegen om de optimale seriegrootte te bepalen.

11.1 Formule van Camp

Een handig model waarmee je de optimale seriegrootte kunt berekenen, is de formule van Camp (uit 1934).

Pas twaalf jaar nadat Camp zijn formule publiceerde, publiceerde Wilson een artikel met dezelfde formule. In Amerikaanse literatuur wordt daardoor de formule voor de economische seriegrootte vaak Wilsons Formula genoemd. In Duitsland noemen ze het Webers Formel.

We zullen het gebruik van de formule van Camp uitleggen aan de hand van een voorbeeld.

Denk aan de voorraad suiker in het schap van een winkel. We nemen aan dat de consumentenvraag naar suiker betrekkelijk gelijkmatig is en geen substantiële seizoensinvloed heeft. De aanvoer verloopt stootsgewijs en de verkoopeenheid is klein ten opzichte van de aanvoerserie.

De winkel verkoopt 50.000 pakken suiker per jaar.

 Besteller Karel beslist dat hij eens per twee weken de voorraad gaat aanvullen met een vaste seriegrootte. Uitgaande van een jaar van 50 weken kiest Karel als bestelhoeveelheid voor

50.000 / 25 = 2.000 pakken suiker per keer.

Over de situatie is verder het volgende bekend:

. de inkoopprijs is  € 0,60 per pak;

. in voorraad houden van een pak suiker gedurende één jaar kost 20% van de inkoopprijs van het artikel (rente, ruimte en risico);

. de orderkosten (de administratieve afhandelingen, de goederenontvangst, etc.) komen op € 4,- per bestelling (per artikel).

Met deze gegevens kan het volgende worden berekend:

• De gemiddelde voorraad is gelijk aan de halve bestelserie (als er geen veiligheidsvoorraad is), dus ½ Q = 1.000 pakken.
• De voorraadwaarde is 1.000 x 0,60 = € 600,-.
• De voorraadkosten (C_v) per jaar zijn: 600 x 20% = € 120,-.
• De order- of bestelkosten (C_b) zijn: 50.000 / 2.000 x € 4,- = € 100,-.
• De totale kosten (C_tot) die met het bestellen van de suiker samen hangen, bedragen per jaar: € 120,- + € 100,- = € 220,- 

De seriegrootte van 2.000 pakken lijkt nogal willekeurig gekozen door Karel. De totale kosten zouden bij een andere ordergrootte wel eens hoger of lager kunnen zijn.

Als Karel de formule van Camp had gebruikt, wat zou dan de ordergrootte zijn?

Minimale kosten

Met het model van Camp vind je het minimum van de totale kosten. Als ‘totale’ kosten worden in dit model de kosten voor het bestellen en de kosten voor het voorraadhouden bij elkaar opgeteld. Het model is dus een beperkte afspiegeling van de werkelijkheid, waarin alleen de twee relevante kosten worden meegenomen, die tegen elkaar moeten worden afgewogen:

C_tot  =  C_bestellen + C_voorraad

Voorraadkosten

We beginnen met het uitdrukken van de jaarlijkse voorraadkosten in een formule, zodat je bij elke waarde van Q kunt berekenen wat de bijbehorende voorraadkosten zijn. We nemen alleen de seriegroottevoorraad mee in de berekening. Veiligheidsvoorraad heeft geen relatie met de seriegrootte. Veiligheidsvoorraden en de kosten daarvan mogen dus geen invloed hebben op de seriegrootte en die laten we daarom buiten ons model.

• De gemiddelde voorraad is gelijk aan de halve seriegrootte: ½ Q.
• De voorraadkosten per product zijn een factor (waarin is begrepen rente, ruimte en risico) maal de kostprijs: a ´ K per jaar.

De totale jaarlijkse voorraadkosten C_v zijn dus in formulevorm weer te geven als:

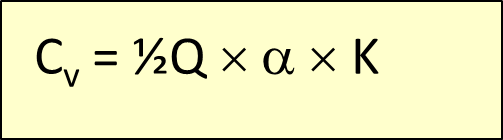
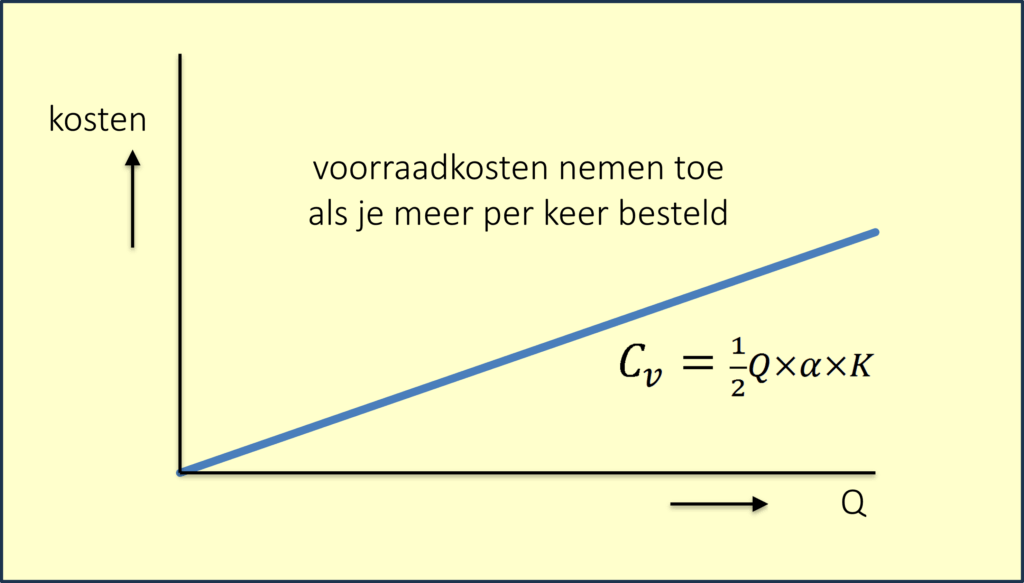
Figuur 9  verband tussen seriegrootte en voorraadkosten

Orderkosten of bestelkosten

Vervolgens drukken we de jaarlijkse orderkosten uit in een formule, zodat we voor elke willekeurige waarde van Q kunnen berekenen wat de bijbehorende bestelkosten zijn.

Per jaar is het aantal bestellingen (of het aantal productieorders als het gaat om fabricage) gelijk aan het totale jaarverbruik, gedeeld door de seriegrootte: D/Q.

De kosten die je per bestelling maakt, noemen we F. Dit zijn of de kosten die ontstaan als je (extern) bij een leverancier bestelt of de kosten die intern ontstaan door het omstellen van machines in de productie van het ene product naar het andere.

De orderkosten per jaar zijn gelijk aan het aantal bestellingen maal de kosten per bestelling:

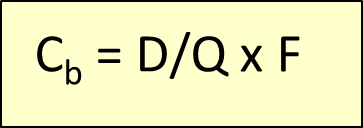
In figuur 10 kun je zien dat de bestelkosten afnemen naarmate je meer per keer bestelt.

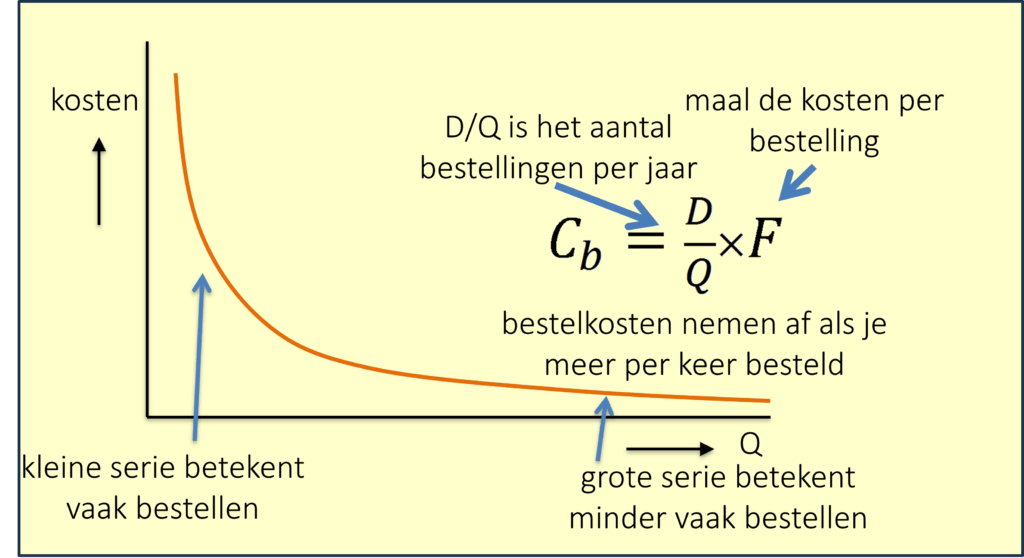
Figuur 10 Verband tussen seriegrootte en bestelkosten (of omstelkosten) 

Totale aan de bestelserie gerelateerde kosten

Als we het hierboven hadden over de bestelkosten en de voorraadkosten, dan bedoelden we de kosten die relevant zijn voor het vraagstuk van de seriegrootte. We zijn immers bezig met het ontwikkelen van een model voor voorraadbeheersing en dan laten we alle andere kosten (gemakshalve) buiten het model. De (voor het model) relevante totale voorraadkosten vind je door het optellen van de hierboven genoemde voorraadkosten en de bestelkosten.

Deze totale kosten C_tot zijn (in formulevorm):

Waarin:

Q    = grootte van de bestelserie

D     = het te verwachten jaarverbruik

F     = order- of bestelkosten per bestelling

a    = factor voor de voorraadkosten per jaar

K     = kostprijs per eenheid product

C_tot   = totale kosten

Onderstaande grafische weergave van deze formule (figuur 11) laat zien dat de totale kostencurve een dal heeft, een minimum. Dat is precies het punt waar we naar zoeken, want op dat punt zijn de totale kosten het laagst. De bijbehorende waarde van Q (op de horizontale as) is de optimale seriegrootte.

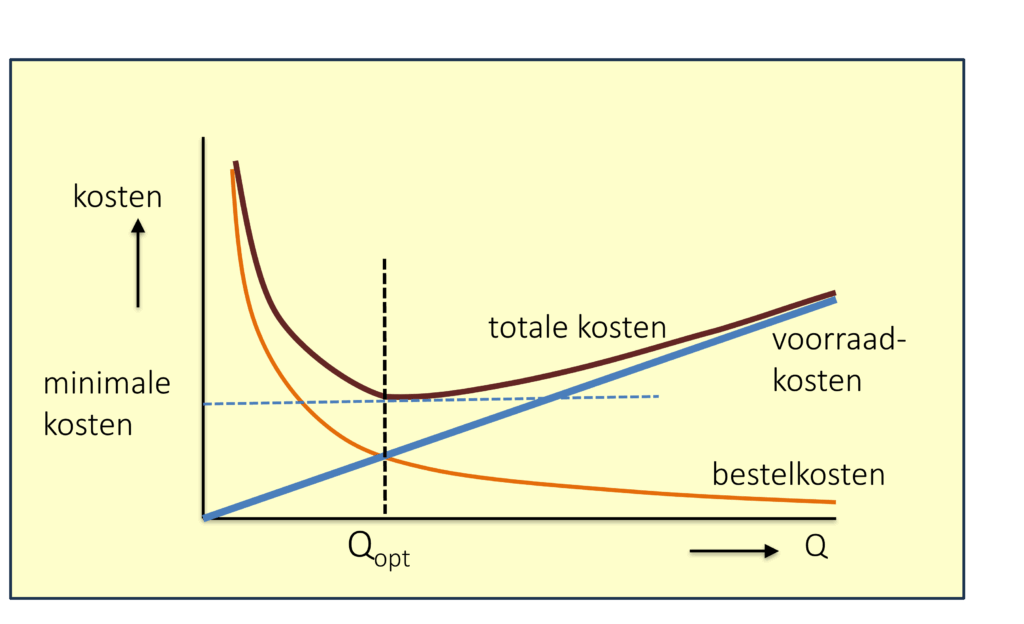
Figuur 11  Voorraadkosten, bestelkosten en de som daarvan samengevoegd in één grafiek

Door de formules over te nemen in Excel kun je een model bouwen, waarmee je de kosten grafieken kunt maken voor verschillende waarden van D, F, a en K.  Deze vier waarden vormen de input van je model, de grafiek toont het minimum van de totale kosten en geeft je inzicht in de gevoeligheid, in de mate waarin de kosten omhoogschieten, als je een beetje meer of minder zou bestellen dan de optimale serie.

Je grafiek gaat er dan bijvoorbeeld zo uitzien als figuur 12.

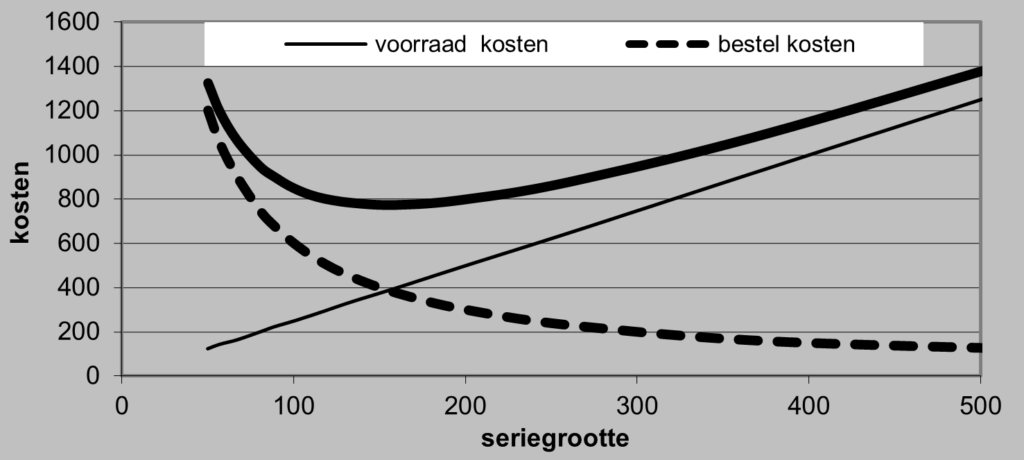
Figuur 12: kostencurven

Het minimum van de totale kosten in de grafiek kun je wiskundig vinden door de functie (de formule) van de totale kosten naar Q te differentiëren en vervolgens de afgeleide functie op nul te stellen. Omdat je in dit specifieke geval (combinatie van rechte lijn en hyperbool) het minimum van de totale kosten ook kunt vinden door te kijken naar het snijpunt van de twee lijnen (waar de voorraadkosten gelijk zijn aan de bestelkosten), kun je de formule ook afleiden door C_v en C_b aan elkaar gelijk te stellen.

We laten de afleidingen in deze module hier buiten beschouwing (we komen er op terug in de Verdieping bij deze Module) en volstaan met het eindresultaat, de formule van Camp

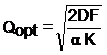
waarin:

Q_opt   = de optimale of economische seriegrootte is. Deze wordt ook wel Q* of EOQ genoemd,
             de (Economic Order Quantity)

D   = de vraag (demand) per jaar

F    = de kosten die een bestelling met zich meebrengt

α    = het percentage voorraadkosten per eenheid per jaar

K    = de kostprijs per eenheid

Terug naar het vraagstuk waar Karel voor stond. Als besteller Karel de formule van Camp had toegepast in het voorbeeld van de suiker, zou hij het volgende resultaat hebben gevonden voor de optimale seriegrootte

Q_opt:

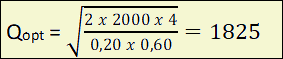
Het zou dus voordeliger uitkomen als Karel in plaats van 2.000 pakken suiker er voortaan 1.825 per keer zou gaan bestellen.