Logicollege

Mogelijk had Karel de berekening met de formule van Camp allang gemaakt en is hij zo slim geweest om de bestelhoeveelheid daarna af te ronden op precies 2 volle pallets van ieder 1.000 pakken.  Hij wist het al, de formule is een hulpmiddel, geen voorschrift.

De formule van Camp levert overigens niet in alle omstandigheden direct de meest economische bestelserie op. Er zijn situaties waarin de formule of het gebruik ervan moet worden aangepast.

1. Als er bij je voorraad verschil is tussen de input- en de outputsnelheid, bijvoorbeeld door een productiesnelheid die afwijkt van je verkoopsnelheid, kan de formule van Camp een verkeerd resultaat opleveren. Daar is een afgeleide formule voor ontwikkeld.

2. Ook als er sprake is van onderhandenwerk of van een seizoenspatroon, kun je niet zonder meer met de formule van Camp werken. Je moet dan correcties in de formule aanbrengen, die ervoor zorgen dat je ook in deze omstandigheden de meest economische seriegrootte berekent.

3. Als er kwantumkortingen spelen, bijvoorbeeld in de vorm van een prijsstaffel, zal een met de formule van Camp berekende seriegrootte waarschijnlijk niet de beste bestelserie zijn. In deze situatie moet je naast de voorraad- en de bestelkosten ook het te behalen prijsvoordeel meewegen. Om tot het beste resultaat te komen, zul je in dit geval voor verschillende staffelniveaus, dus verschillende keren, met de formule moeten werken.

We noemen hierboven drie situaties waarin de formule van Camp geen juist resultaat oplevert, maar er zijn er meer. We gaan daar verder op in, in de Verdieping bij deze Module.

De formule van Camp is een handig model om op basis van beperkte gegevens (afzet, voorraadkosten en order- of bestelkosten) de economische seriegrootte berekenen. In de praktijk zul je door allerlei invloeden van buitenaf vaak moeten afwijken van de berekende optimale seriegrootte en dan zul je merken dat een kleine afwijking van Q* niet zo’n grote invloed heeft op de totale kosten. Bijvoorbeeld door de te bestellen hoeveelheid af te ronden tot een ‘handig’ getal (dat wel in de buurt komt van het berekende optimum). Als je daardoor uitkomt op bijvoorbeeld een hele omverpakking, een heel aantal pallets of een hele containerlading, zal je afronding zelfs een gunstig effect hebben op de totale kosten.

Je zag al eerder, dat de curve van de totale kosten rondom het minimum tamelijk vlak verloopt en pas omhoogschiet als je seriegrootte behoorlijk ver afwijkt van de EOQ. Bij twijfel, bijvoorbeeld als het gaat om kostbare producten of hoge bestelkosten, is het raadzaam om de gevoeligheid van het optimum nader te onderzoeken. Bijvoorbeeld door de grafiek te maken van de kostenlijnen (zoals in je eerder zag in figuur 12). Aan het verloop van de lijn met de ‘totale kosten’ kun je zien of het gebied rondom het minimum tamelijk vlak is (lage gevoeligheid) of juist steil omhoog gaat (grote gevoeligheid). In de figuren 13 en 14 laten we dit zien.

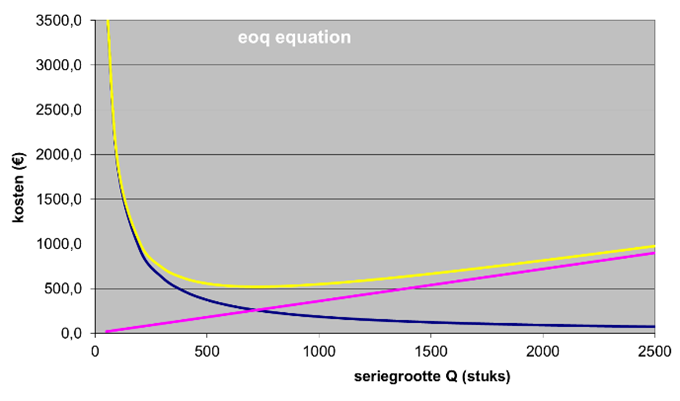
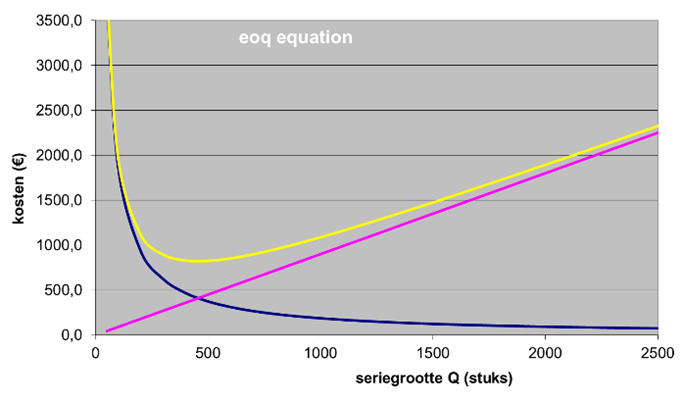
Figuur 13 tamelijk ongevoelige EOQ                                figuur 14 gevoelige EOQ

De grafiek in figuur 13 is gebaseerd op D=2500, B=75, K=18 en α=4%. De EOQ is in dit geval 722. De gele lijn met de ‘totale kosten’ laat een nogal vlak verloop zien rondom het minimum. Voor figuur 14 zijn dezelfde uitgangspunten gebruikt, alleen zijn de voorraadkosten (α) nu gesteld op 10%. Dat heeft grote invloed: de EOQ is nu 456 en is veel gevoeliger voor aanpassing van de bestelserie.

In veel gevallen zijn afwijkingen van de optimale seriegrootte zijn te rechtvaardigen. We noemen daar een aantal voorbeelden van:

• Als er beperkte opslagruimte is in je magazijn.
• Als het gaat om erg veel volume bij opslag en bij transport, bijvoorbeeld bij isolatiemateriaal.
• Als je beter een volle container (FCL) kunt bestellen gezien de relatief hoge transportkosten van een gedeeltelijke containerlading (LCL).
• Bij producten met beperkte houdbaarheid. De berekende optimale serie zou kunnen leiden tot een te lange doorlooptijd van je voorraad, met bederf tot gevolg.
• Om af te ronden op hele verpakkingseenheden waarin de goederen geleverd worden. Bijvoorbeeld een vat, een doos, een pallet, een container.
• Vanwege geplande wijzigingen van de stuklijst van je eindproduct, wil je minder onderdelen inkopen dan de optimale serie aangeeft.
• Als je de seriegrootte zou kunnen aanpassen aan de standtijd van gereedschappen vanwege de daarmee gepaard gaande kosten. Onder de standtijd verstaan we het aantal producten dat onder normale omstandigheden bewerkt kan worden, voordat het gereedschap moet worden verwisseld. Bijvoorbeeld een beitel of een frees die moet worden geslepen.
• Omdat je strikte uniforme beheersnormen per categorie hebt gesteld, bijvoorbeeld na indeling van je assortiment in A-, B- en C-categorieën. Je zou er bijvoorbeeld voor kunnen kiezen om de voorraad van alle C-artikelen maar eenmaal per maand te toetsen en voor al deze artikelen als seriegrootte het gemiddeld verbruik 3 maanden te hanteren (sQ-systeem). Je leverancier zal blij zijn met de wat grotere orders en de regelmaat en doet wellicht daarom nog wat van de prijs af.
• Als de liquiditeit van de onderneming laag is, als geld schaars is. Maar dan kun je beter een hogere factor a in de formule van Camp moeten kiezen, want in dit geval is geld dat vastligt in voorraad wellicht harder nodig voor iets anders. Geld is dan duur.
• Vanwege de product lifecycle, als bijvoorbeeld sprake is van een uitlopend artikel, kun je maar beter voorzichtig zijn met een nieuwe serie.
• Als sprake is van grote veranderingen in de vraag, want met kleinere series voorkom je dat je met overschotten blijft zitten. Een tweede reden is dat de leadtime van kleinere orders waarschijnlijk korter zal zijn, waardoor je met je voorraad sneller op de vraagfluctuaties kunt reageren.